Funciones LAMBDA: REDUCE, MAP, SCAN, BYCOL, BYROW

Si la función LAMBDA ha sido un paso de gigante para Excel, no podemos olvidarnos del paquete de funciones que vienen con ella: REDUCE, MAP, SCAN, BYCOL, BYROW o MAKEARRAY

En general todas estas funciones tienen la peculiaridad de trabajar, de una forma u otra sobre matrices de información, a las que aplica una transformación empleando la función LAMBDA.
De alguna manera podríamos decir que se comportan a modo de bucle o recorrido por los valores de la matriz dada.
Conozcamóslas...
BYCOL: Aplica LAMBDA a cada columna y devuelve un vector columna con los resultados de la transformación resultante de Lambda.
Su sintáxis es muy sencilla:
=BYCOL(columna; LAMBDA(columna))

BYROW: Aplica LAMBDA a cada fila y devuelve un vector columna con los resultados de la transformación resultante de Lambda.
Su sintáxis es muy sencilla:
=BYROW(fila; LAMBDA(fila))

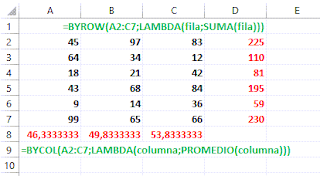
Veamos un ejemplo de estas sencillas funciones... Si disponemos de un matriz de valores en A2:C7 y queremos obtener una fila y una columna de subtotales:

Al añadir en la celda D2 la función:
=BYROW(A2:C7;LAMBDA(fila;SUMA(fila)))
obtenemos un vector de valores que recorre nuestra matriz, recuperando para cada fila la operación deseada.
De forma similar en la celda A8 insertamos:
=BYCOL(A2:C7;LAMBDA(columna;PROMEDIO(columna)))
obteniendo un vector donde asocia para cada columna el cálculo descrito por Lambda.

Otra de las funciones es MAKEARRAY ('traducida' en español como 'ARCHIVOMAKEARRAY' por qué???): Que nos devuelve una matriz calculada de un tamaño de fila y columna especificado, aplicando LAMBDA a cada elemento de dicha matriz.
Su sintáxis sería:
=MAKEARRAY(filas; columnas; LAMBDA(fila; columna))

Un ejemplo simple nos permitiría crear una matriz que identifique cada elemento de la matriz por sus posiciones (fila 1 - col 1, fila 1- col 2, fila 2 - col 1, etc...)
En cualquier celda escribiríamos:
=ARCHIVOMAKEARRAY(3;2;LAMBDA(fila;col;--(fila&col)))
con lo que obtenemos una matriz de 3 filas x 2 columnas y como elementos su identificación de fila&columna

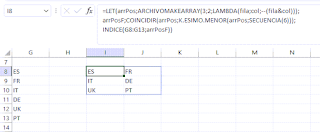
Un ejemplo más elaborado de esta función nos permitiría convertir un vector en una matriz...
Como vemos en la imagen, a partir del vector en G8:G13, podemos obtener la matriz siguiente:

La fórmula empleada para llegar a este resultado es:
=LET(arrPos;ARCHIVOMAKEARRAY(3;2;LAMBDA(fila;col;--(fila&col)));
arrPosF;COINCIDIR(arrPos;K.ESIMO.MENOR(arrPos;SECUENCIA(6)));
INDICE(G8:G13;arrPosF))
Puedes echar un vistazo al artículo publicado hace algún tiempo en este blog.

Otras funciones más interesantes de las que disponemos serían...

MAP: Devuelve una matriz formada por la asignación de cada valor de las matrices a un nuevo valor aplicando LAMBDA para crear un nuevo valor.
Su sintáxis:
=MAP(array1; LAMBDA_o_array)
Esta función, en definitiva recorre cada elemento ('mapea') de la matriz, aplicándole la transformación indicada con LAMBDA, y recuperando una matriz de igual dimensión tratada...
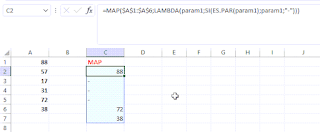
Por ejemplo

La fórmula aplicada:
=MAP($A$1:$A$6;LAMBDA(param1;SI(ES.PAR(param1);param1;"-")))
recorre la matriz aplicando el condicional indicado por LAMBDA, determinando si es par o no...

LLegamos a las funciones interesantes de verdad...
La siguiente función SCAN examina una matriz aplicando LAMBDA a cada valor y devuelve una matriz que tiene cada valor intermedio.
La sintáxis será:
SCAN ([initial_value]; array; LAMBDA(accumulator; value))
donde:
[initial_value]: establece el valor inicial del acumulador.
array: matriz que se va a examinar.
función LAMBDA a la que se llama para examinar la matriz. Y sus dos importantes parámetros:
accumulator: Valor total y devuelto como resultado final.
value: Cálculo aplicado a cada elemento de la matriz.

Con SCAN conseguimos una matriz con valores secuenciales, calculados en base al resultado previo obtenido por la aplicación de LAMBDA...
Por ejemplo, un acumulado creciente (running total) en valores absolutos y en valores porcentuales.

Las fórmulas aplicadas son:
En C2 añadimos:
=SCAN(0;A1:A6;LAMBDA(acum;param1;acum+param1))
y en D2 insertamos:
=LET(total;SUMA(A1:A6);SCAN(0;A1:A6;LAMBDA(acum;param1;(acum+param1)))/total)

Y por fin, desde mi punto de vista la más importante de todas, nuestra última función es REDUCE, la cual reduce una matriz a un valor acumulado aplicando LAMBDA a cada valor y devolviendo el valor total en el acumulador.
Esto es, hace algo similar a lo que desarrolla SCAN, pero solo retorna la última transformación.. después de todos los pasos intermedios aplicados.
Nuestra sintáxis:
=REDUCE([initial_value]; array; LAMBDA(accumulator; value))
donde:
[initial_value]: establece el valor inicial del acumulador.
array: matriz que se va a 'reducir'.
función LAMBDA a la que se llama para reducir. Y sus dos importantes parámetros:
accumulator: Valor total y devuelto como resultado final.
value: Cálculo aplicado a cada elemento de la matriz.

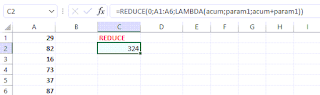
Por ejemplo, para recuperar el valor acumulado último de una suma corrida

La fórmula del ejemplo es:
=REDUCE(0;A1:A6;LAMBDA(acum;param1;acum+param1))
Quizá pienses que es poco útil y muy 'tonta', pero esta función nos permite aplicar recorridos sobre matrices y trabajar sobre el resultado previo, para de nuevo aplicar la siguiente operación... En definitiva, nos abre un mundo de movimientos y operaciones recursivas...
Lo cual veremos en la siguiente entrada ;-)