Convertir Vector en Matriz

Revisaremos en el artículo de hoy algunas alternativas para convertir, mediante fórmulas, un vector de celdas en una matriz de n filas x m columnas.

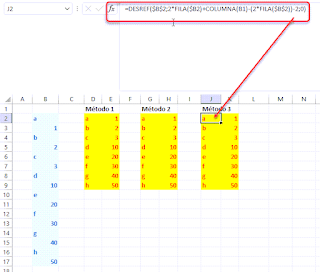
Veremos tres métodos para la conversión buscada, i.e., para llegar del rango/vector B2:B17 a la matriz de 8 filas x 2 cols (de los rango en amarillo, en la imagen anterior).

El primer método sería el más general y quizá novedoso (no lo he visto nunca, y di con él probando otro desarrollo), ya que aunque estoy empleando la funcion LET, se podría reproducir con el empleo de nombres definidos, o incluso en una fórmula tradicional...
En D2 escribiríamos:

  =LET(
       arrPosicion;--LET(vector;$B$2:$B$17;
       vFilas;FILA(INDIRECTO("1:8"));
       vCols;TRANSPONER(FILA(INDIRECTO("1:2")));
       (vFilas&vCols));
vPosicion;K.ESIMO.MENOR(arrPosicion;FILA(INDIRECTO("1:16")));
rankPosicion;COINCIDIR(arrPosicion;vPosicion;0);
INDICE($B$2:$B$17;rankPosicion))

Lo interesante del proceso de cálculo son las etapas iniciales, donde se compone una matriz de 8 filas x 2 cols basados en un concatenado de posiciones de filas y columnas, como se vé en la imagen siguiente:

arrPosicion;--LET(vector;$B$2:$B$17;
       vFilas;FILA(INDIRECTO("1:8"));
       vCols;TRANSPONER(FILA(INDIRECTO("1:2")));
       (vFilas&vCols))

Esta disposición de valores nos permite en el paso siguiente obtener un vector ordenado de posiciones, ordenados de menos a más y siguiendo el orden de filas, es decir, un vector columna: 11,12,21,2,31,32, ... , 81,82:

vPosicion;K.ESIMO.MENOR(arrPosicion;FILA(INDIRECTO("1:16")))

En un paso siguiente, reconvertimos en una serie del 1 al 16 cada valor del vector anterior... es decir, pasamos de la matriz arrPosicion
11 12
21 22
31 32
41 42
51 52
61 62
71 72
81 82
a la matriz:
1 2
3 4
5 6
7 8
9 10
11 12
13 14
15 16
Justo lo que necesitamos para añadir al argumento de la función INDICE:

INDICE($B$2:$B$17;rankPosicion)

Con lo que llegamos al resultado deseado!! :O

El segundo método es mucho más simple, ya que se basa en el uso combinado de INDICE y SECUENCIA.
Siendo SECUENCIA la encargada de construir la matriz necesaria de posiciones. En G2 escribimos:

=INDICE($B$2:$B$17;SECUENCIA(8;2))

Mucha más simple y fácil de escribir y analizar...pero requiere de la función SECUENCIA actualmente solo disponible en Microsoft 365 :'(

Un tercer método sería empleando la función DESREF, anidando en ella las clásicas funciones FILA, COLUMNA; y necesita que seamos nosotros quienes nos encarguemos de copiar y pegar la fórmula (o arrastrar) sobre el rango final esperado.
En J2 podríamos escribir:

=DESREF($B$2;2*FILA($B2)+COLUMNA(B1)-(2*FILA($B$2))-2;0)

No olvides arrastrar desde J2 hasta K9!!!.
En este ejemplo, con el uso de la fórmula:
2*FILA($B2)+COLUMNA(B1)-(2*FILA($B$2))-2
conseguiríamos una matriz de posiciones, desde la celda B2, para obtener en el orden adecuado, cada valor en su correcta posición 'matricial':
0 1
2 3
4 5
6 7
8 9
10 11
12 13
14 15
esto es, desde B2 nos desplazamos cero filas, cero columnas... por tanto recupero, el dato de B2. Que ubico en la posición matricial fila 1 - columna 1
para el siguiente, desde B2 nos desplazamos 1 fila, cero columnas, y recupero el dato de B3. Que ubico en la posición matricial fila 1 - columna 2
para el siguiente, desde B2 nos desplazamos 2 filaa, cero columnas, y recupero el dato de B4. Que ubico en la posición matricial fila 2 - columna 1
Y sucesivamente... concluyendo con la matriz de celdas buscadas...

Seguro que habrá formas más vistosas, o incluso fáciles... pero es un buen recopilatorio de métodos para pasar de Vector a Matriz.