Hoy toca un poco de programación en VBA para Excel.
Aprovechando un tema siempre interesante: el cuadrado mágico de Euler que reune dos temas apasionantes.. secuencias matemáticas y ajedrez, veremos algunas rutinas de macros interesantes.
En qué consiste este cuadrado 'semimágico' de Euler...
/ Este gran matemático (el del número e) fue capaz de montar la secuencia natural de números del 1 al 64 sobre un tablera de ajedrez (8 x 8 = 64 escaques) distribuidos siguiendo la secuencia de movimientos de un caballo (la figura del ajedrez)!!!.
No solo eso, además cada fila y columna de sus secuencia distribuida sumarán siempre 260... pero encima, si dividimos en cuatro cuadrados de 4 x 4 nuestro tablero, cada parte suma igualmente una misma cantidad: 520 (si, el doble de 260)... increible!!.
Solo le falto que las diagonales también sumaran esos 260 para conseguir el perfecto cuadrado mágico... no se puede tener todo, verdad?.
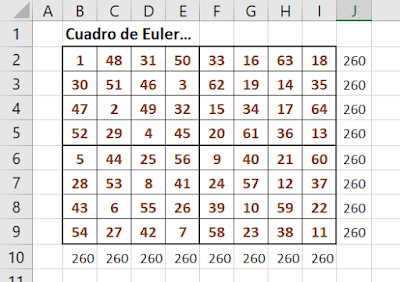
Los valores de este cuadrado:
Nuestra experiencia de hoy será replicar el camino que seguiría ese caballo por el tablero, siguiendo el orden natural 1,2,3,4,..., 64. Mostrando con flechas y colores esos movimientos.
Para ello emplearemos un truco que simula una matriz de constantes con los ocho movimientos posibles de un caballo; y por otro lado usaremos el método Shapes.Addline para añadir con flechas dichos movimientos...
Insertamos un módulo en nuestro proyecto, y en el añadimos nuestro procedimiento auxiliar que permite añadir las flechas:
De especial interes cómo hemos definido la matriz de movimientos:
'definimos la matriz de constantes de ocho movimientos del caballo posibles... arrMovs = [{1, -1, 2, 2, 1, -1, -2, -2; 2, 2, 1, -1, -2, -2, 1, -1}]
con dos filas y ocho columnas, desde la que posteriormente poder recuperar sus pares de valores con la notación:
fB = arrMovs(1, x)
cB = arrMovs(2, x)
El resto del código no parece tener especial dificultad, ya que solo son bucles y condicionales que permiten seleccionar las celdas e ir coloreándolas...
De otra parte, para insertar las líneas, empleamos el método:
'expresión. AddLine (BeginX, BeginY, EndX, Endy)
donde definimos el inicio y fin con las propiedades .Top, .Left, .Width y .Height de Range.
El resultado se puede ver, en el video al inicio del post.
Espero te haya resultado interesante ;-)
Aprovechando un tema siempre interesante: el cuadrado mágico de Euler que reune dos temas apasionantes.. secuencias matemáticas y ajedrez, veremos algunas rutinas de macros interesantes.
En qué consiste este cuadrado 'semimágico' de Euler...
/ Este gran matemático (el del número e) fue capaz de montar la secuencia natural de números del 1 al 64 sobre un tablera de ajedrez (8 x 8 = 64 escaques) distribuidos siguiendo la secuencia de movimientos de un caballo (la figura del ajedrez)!!!.
No solo eso, además cada fila y columna de sus secuencia distribuida sumarán siempre 260... pero encima, si dividimos en cuatro cuadrados de 4 x 4 nuestro tablero, cada parte suma igualmente una misma cantidad: 520 (si, el doble de 260)... increible!!.
Solo le falto que las diagonales también sumaran esos 260 para conseguir el perfecto cuadrado mágico... no se puede tener todo, verdad?.
Los valores de este cuadrado:
Nuestra experiencia de hoy será replicar el camino que seguiría ese caballo por el tablero, siguiendo el orden natural 1,2,3,4,..., 64. Mostrando con flechas y colores esos movimientos.
Para ello emplearemos un truco que simula una matriz de constantes con los ocho movimientos posibles de un caballo; y por otro lado usaremos el método Shapes.Addline para añadir con flechas dichos movimientos...
Insertamos un módulo en nuestro proyecto, y en el añadimos nuestro procedimiento auxiliar que permite añadir las flechas:
Sub AñadimosFlecha(FromCell As Range, ToCell As Range) iniX = FromCell.Left + (FromCell.Width / 2) iniY = FromCell.Top + (FromCell.Height / 2) finX = (ToCell.Left + (ToCell.Width / 2)) finY = (ToCell.Top + (ToCell.Height / 2)) 'expresión. AddLine (BeginX, BeginY, EndX, Endy) Set flecha = FromCell.Parent.Shapes.AddLine(iniX, iniY, finX, finY) 'seleccionamos la linea flecha.Select 'y añadimos la terminación en forma de flecha Selection.ShapeRange.Line.EndArrowheadStyle = msoArrowheadTriangle End SubPor otra parte, en el mismo módulo, añadimos el procedimiento Sub principal:
Sub Euler()
'dejamos celdas sin color
Range("ndEuler").Interior.Color = xlNone
'y eliiminamos las formas...
Dim shp As Shape
For Each shp In ActiveSheet.Shapes
shp.Delete
Next shp
'limites filas y columnas del cuadro
fila1 = Range("ndEuler").Row
fila8 = fila1 + 8 - 1
col1 = Range("ndEuler").Column
col8 = col1 + 8 - 1
'situación inicio
Range("ndEuler").Cells(1, 1).Select
Selection.Interior.Color = vbCyan
Application.Wait (Now + TimeValue("0:00:02") / 3)
Selection.Interior.Color = vbYellow
ValorActual = Selection.Value
'nos movemos, y probamos encontrar el valor siguiente al Actual
'con el movimiento del caballo!!
'definimos la matriz de constantes de ocho movimientos del caballo posibles...
arrMovs = [{1, -1, 2, 2, 1, -1, -2, -2; 2, 2, 1, -1, -2, -2, 1, -1}]
Dim horizontal As Integer, vertical As Integer, x As Integer, i As Integer
'forzamos los 64 escaques posibles
For i = 1 To 64
For x = 1 To UBound(arrMovs, 2)
fA = Selection.Row
cA = Selection.Column
fB = arrMovs(1, x)
cB = arrMovs(2, x)
'control dentro cuadro
If fA + fB >= fila1 And fA + fB <= fila8 And _
cA + cB >= col1 And cA + cB <= col8 Then
'si el movimiento cae dentro del cuador
If Selection.Value + 1 = Selection.Offset(fB, cB).Value Then
'y además el valor encontrado es el siguiente...
'y añadimos los conectores
Call AñadimosFlecha(Cells(fA, cA), Cells(fA, cA).Offset(fB, cB))
Cells(fA, cA).Select
'marcamos la celda final
Selection.Offset(fB, cB).Select
Selection.Interior.Color = vbCyan
'damos un retraso de tiempo para resaltar el cambio
Application.Wait (Now + TimeValue("0:00:02") / 3)
Selection.Interior.Color = vbYellow
'seleccionamos celda última con valor
Cells(fA, cA).Offset(fB, cB).Select
End If
End If
Next x
Next i
End Sub
Notemos que previamente he asignado al cuadrado o rango de celdas B2:I9 el nombre definido: 'ndEuler'.De especial interes cómo hemos definido la matriz de movimientos:
'definimos la matriz de constantes de ocho movimientos del caballo posibles... arrMovs = [{1, -1, 2, 2, 1, -1, -2, -2; 2, 2, 1, -1, -2, -2, 1, -1}]
con dos filas y ocho columnas, desde la que posteriormente poder recuperar sus pares de valores con la notación:
fB = arrMovs(1, x)
cB = arrMovs(2, x)
El resto del código no parece tener especial dificultad, ya que solo son bucles y condicionales que permiten seleccionar las celdas e ir coloreándolas...
De otra parte, para insertar las líneas, empleamos el método:
'expresión. AddLine (BeginX, BeginY, EndX, Endy)
donde definimos el inicio y fin con las propiedades .Top, .Left, .Width y .Height de Range.
El resultado se puede ver, en el video al inicio del post.
Espero te haya resultado interesante ;-)



No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.