Hoy toca algo de formulación específica para el cálculo de desviaciones, pero solo para los meses consecutivos.
Se trata a partir de un listado de fechas, llegar al porcentaje de desviación de los importes acumulados por mes, solo en los casos de meses correlativos.
Algo muy concreto pero interesante por un par de técnicas de construcción de fórmulas complejas.
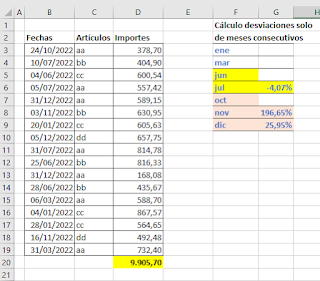
¿Qué vemos en la imagen anterior?
Cómo, con una única fórmula, se ha conseguido procesar los datos listados para internamente:
primero - acumular por mes los importes correspondientes.
segundo - calcular las desviaciones sobre los importes acumulados... si cumplen la condición de ser consecutivos. tercero - retornar únicamente los meses en texto y las desviaciones calculadas.
Veamos la 'formulita' en cuestión:
El proceso es simple...
Comenzamos, con la función LET, declarando y definiendo las variables/rangos sobre los que vamos a trabajar:
Continuamos procesando los rangos anteriores con la función MAP, la que nos permitirá obtener los importes acumulados por cada mes de nuestro listado.
Seguidamente compondremos una matriz de resultados con APILARH, uniendo el listado numérico de meses al recién calculado vector de importes acumulados.
Sobre esta matriz resultante, aplicaremos un nuevo proceso, evaluando la condición sobre el listado de meses ordenado de la primera columna de la matriz anterior, y solo en el caso de que sean meses consecutivos, i.e., que el mes previo sea igual al actual mas uno, aplicar el cálculo clásico de desviaciones mes_presente / mes_anterior -1
Concluimos nuestra fórmula juntando, otra vez con APILARH los meses ya convertidos a TEXTO, junto a los porcentajes de desviación obtenido.
Tenemos pues las pistas para obtener cálculos complejos.
1-declarar variables
2-realizar cálculos intermedios
3-concluir el cálculo con los valores anteriores.
Espero te haya resultado interesante... y quedo abierto a cualquier sugerencia ;-)
Se trata a partir de un listado de fechas, llegar al porcentaje de desviación de los importes acumulados por mes, solo en los casos de meses correlativos.
Algo muy concreto pero interesante por un par de técnicas de construcción de fórmulas complejas.
¿Qué vemos en la imagen anterior?
Cómo, con una única fórmula, se ha conseguido procesar los datos listados para internamente:
primero - acumular por mes los importes correspondientes.
segundo - calcular las desviaciones sobre los importes acumulados... si cumplen la condición de ser consecutivos. tercero - retornar únicamente los meses en texto y las desviaciones calculadas.
Veamos la 'formulita' en cuestión:
=LET(datos;$B$3:$D$19;
datos_ordenados; ORDENAR(datos; 1; 1);
fechas;INDICE(datos_ordenados;0;1);
importes;INDICE(datos_ordenados;0;3);
convertido;UNICOS(MES(fechas));
acumulado; MAP(SECUENCIA(FILAS(convertido));
LAMBDA(fila; SUMAPRODUCTO(importes*( MES(fechas)=INDICE(convertido;fila;1)))));
rdo;APILARH(convertido;acumulado);
variacion; MAP(SECUENCIA(FILAS(rdo)); LAMBDA(fila2;
SI( Y(INDICE(rdo; fila2; 1)=INDICE(rdo; fila2-1; 1)+1);
(INDICE(rdo; fila2; 2) / INDICE(rdo; fila2-1;2) )- 1; "") ) );
APILARH(TEXTO(FECHA(2022;EXCLUIR(rdo;;-1);1);"mmm");variacion) )El proceso es simple...
Comenzamos, con la función LET, declarando y definiendo las variables/rangos sobre los que vamos a trabajar:
=LET(datos;$B$3:$D$19;
datos_ordenados; ORDENAR(datos; 1; 1);
fechas;INDICE(datos_ordenados;0;1);
importes;INDICE(datos_ordenados;0;3);
convertido;UNICOS(MES(fechas));...Continuamos procesando los rangos anteriores con la función MAP, la que nos permitirá obtener los importes acumulados por cada mes de nuestro listado.
...
acumulado; MAP(SECUENCIA(FILAS(convertido));
LAMBDA(fila; SUMAPRODUCTO(importes*( MES(fechas)=INDICE(convertido;fila;1)))));
...Seguidamente compondremos una matriz de resultados con APILARH, uniendo el listado numérico de meses al recién calculado vector de importes acumulados.
...
rdo;APILARH(convertido;acumulado);
...Sobre esta matriz resultante, aplicaremos un nuevo proceso, evaluando la condición sobre el listado de meses ordenado de la primera columna de la matriz anterior, y solo en el caso de que sean meses consecutivos, i.e., que el mes previo sea igual al actual mas uno, aplicar el cálculo clásico de desviaciones mes_presente / mes_anterior -1
...
variacion; MAP(SECUENCIA(FILAS(rdo)); LAMBDA(fila2;
SI( Y(INDICE(rdo; fila2; 1)=INDICE(rdo; fila2-1; 1)+1);
(INDICE(rdo; fila2; 2) / INDICE(rdo; fila2-1;2) )- 1; "") ) );
...Concluimos nuestra fórmula juntando, otra vez con APILARH los meses ya convertidos a TEXTO, junto a los porcentajes de desviación obtenido.
...
APILARH(TEXTO(FECHA(2022;EXCLUIR(rdo;;-1);1);"mmm");variacion)
...Tenemos pues las pistas para obtener cálculos complejos.
1-declarar variables
2-realizar cálculos intermedios
3-concluir el cálculo con los valores anteriores.
Espero te haya resultado interesante... y quedo abierto a cualquier sugerencia ;-)


No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.