En la entrada anterior del blog hablabamos de las funciones recursivas, y mencionabamos alternativas como:
List.Acumulate o List.Generate
Replicaremos el ejemplo del post comentado: crear la Secuencia de Fibonacci con la función List.Generate y List.Accumulate.
Así pues, para llegar a la misma Secuencia de Fibonacci empleando la función List.Generate:
¿Qué hace List.Generate en nuestro ejemplo?:
- Primero define el punto de partida. Un registro con dos variables:
()=>[anterior=0, actual=1],
- En segundo lugar damos una condición de avance o de salida!!! (fundamental!!):
each [anterior] + [actual] < 47000,
para nosotros, mientras el valor de la Secuencia de Fibonacci sea inferior a 47.000
- En tercer lugar informamos cuáles serán los siguientes valores (mientras cumplan la condición del argumento previo).
Generamos un nuevo Registro a partir de los datos anteriores, i.e., reasignamos valores a nuestra dupla:
each [anterior=[actual], actual=[anterior] + [actual]],
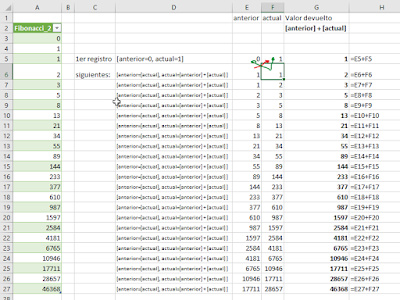
En la imagen anterior replicamos el proceso interno de List.Generate
- Finalizamos dando el dato a devolver:
each [anterior] + [actual]
suma de ambas variables de nuestro Registro.
Para completar la serie incluimos manualmente los elementos primeros: 0 y 1:
List.Union({{0,1} & Fibonacci2})
Obteniendo finalmente nuestra Secuencia de Fibonacci esperada...
Un ejercicio similar con List.Accumulate sería el siguiente:
O también...
En ambos casos alimentamos List.Accumulate con una lista variable que empleamos para asignar al Acumulador... siguiendo igual dinámica que con el ejemplo de List.Generate.
Seguramente exista alguna otra forma más eficiente, para ambas funciones M... pero estos ejemplos muestran las alternativas de que disponemos frente a las funciones recursivas (más complejas conceptualmente).
List.Acumulate o List.Generate
Replicaremos el ejemplo del post comentado: crear la Secuencia de Fibonacci con la función List.Generate y List.Accumulate.
Así pues, para llegar a la misma Secuencia de Fibonacci empleando la función List.Generate:
let
//No hace falta partir de una lista,
// ya que List.Generate la crea por nosotros...
// List.Generate(initial as function, condition as function, next as function, optional selector as nullable function) as list
//Algortimo de Fibonacci, esto es, acumulando el valor presente al anterior
Fibonacci2=List.Generate(
()=>[anterior=0, actual=1], // punto de partida: Dos variables definidas en un Registro.
each [anterior] + [actual] < 47000, // condición - control de salida!!!
each [anterior=[actual], actual=[anterior] + [actual]], // siguiente valor. Nuevo Registro
each [anterior] + [actual] // el Selector determina que valor a devolver
),
Completa=List.Union({{0,1} & Fibonacci2}) // forzando como primeros elementos el 0 y el 1
in
Completa¿Qué hace List.Generate en nuestro ejemplo?:
- Primero define el punto de partida. Un registro con dos variables:
()=>[anterior=0, actual=1],
- En segundo lugar damos una condición de avance o de salida!!! (fundamental!!):
each [anterior] + [actual] < 47000,
para nosotros, mientras el valor de la Secuencia de Fibonacci sea inferior a 47.000
- En tercer lugar informamos cuáles serán los siguientes valores (mientras cumplan la condición del argumento previo).
Generamos un nuevo Registro a partir de los datos anteriores, i.e., reasignamos valores a nuestra dupla:
each [anterior=[actual], actual=[anterior] + [actual]],
En la imagen anterior replicamos el proceso interno de List.Generate
- Finalizamos dando el dato a devolver:
each [anterior] + [actual]
suma de ambas variables de nuestro Registro.
Para completar la serie incluimos manualmente los elementos primeros: 0 y 1:
List.Union({{0,1} & Fibonacci2})
Obteniendo finalmente nuestra Secuencia de Fibonacci esperada...
Un ejercicio similar con List.Accumulate sería el siguiente:
let
// List.Accumulate(list as list, seed as any, accumulator as function) as any
// Acumula un valor de resumen de los elementos de la lista list, mediante accumulator. Se puede establecer un parámetro de inicialización opcional, seed.
//Algortimo de Fibonacci, esto es, acumulando el valor presente al anterior
Fibonacci3=List.Transform({0..24}, // creamos una lista para alimentar el Acumulado
(x) => let Fibo =(n) => List.Accumulate(
List.Generate(()=>0, each _<x-1, each _+1), //Lista variable para acumular en cada paso
[anterior=0, actual=1], // valores por donde comenzamos. Registro doble anterior / actual
(state, current) => [anterior = state[actual], actual = state[actual] + state[anterior]] //Acumulador que aumenta / da valores al Registro doble anterior / actual (incrementa teniendo en cuenta el dato previo)
)
in
Record.ToList( Fibo(x) ) ), //pasamos cada registro a tipo lista
Completa = List.Union((Fibonacci3)) // y acabamos Uniendo (y eliminando duplicados) todos los registros. Obteniendo un listado de valores únicos que representa la Secuencia de Fibonacci
in
CompletaO también...
let
// List.Accumulate(list as list, seed as any, accumulator as function) as any
// Acumula un valor de resumen de los elementos de la lista list, mediante accumulator. Se puede establecer un parámetro de inicialización opcional, seed.
//Algortimo de Fibonacci, esto es, acumulando el valor presente al anterior
Fibonacci3=List.Transform({1..25}, // creamos una lista para alimentar el Acumulado
(x) => let Fibo =(n) => List.Accumulate(
List.Generate(()=>0, each _<x-1, each _+1), //Lista variable para acumular en cada paso
[anterior=0, actual=1], // valores por donde comenzamos. Registro doble anterior / actual
(state, current) => [anterior = state[actual], actual = state[actual] + state[anterior]] //Acumulador que aumenta / da valores al Registro doble anterior / actual (incrementa teniendo en cuenta el dato previo)
)
in
Fibo(x)[anterior] ) //recuperamos el dato del registro Anterior... para elemento calculado
in
Fibonacci3En ambos casos alimentamos List.Accumulate con una lista variable que empleamos para asignar al Acumulador... siguiendo igual dinámica que con el ejemplo de List.Generate.
Seguramente exista alguna otra forma más eficiente, para ambas funciones M... pero estos ejemplos muestran las alternativas de que disponemos frente a las funciones recursivas (más complejas conceptualmente).


No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.