Contar en rangos NO adyacentes

Hoy toca algo de formulación que nos ayudará a realizar conteos sobre rangos No adyacentes

El objetivo será lograr contar coincidencias sobre rango no continuos tal y como se ve en la imagen anterior... El asunto no es tan simple como emplear funciones ya conocidas como CONTAR.SI o CONTAR.SI.CONJUNTO, y para dar solución mostraré alternativas con funciones como SUMAPRODUCTO, INDIRECTO o ELEGIR.

En primer lugar haremos uso de una fórmula ya empleada en este post, donde incluimos o asignamos la fórmula siguiente en un nombre definido 'ndProblemas':
ndProblemas = =LET(
rangos;(Tabla1[problema1];Tabla1[problema2];Tabla1[problema3]);
Areas;AREAS(rangos);
filas;FILAS(Tabla1[problema1]);
TotalFilas;SECUENCIA(Areas*filas);
NumArea;MULTIPLO.SUPERIOR.MAT(SECUENCIA(Areas*filas);filas)/filas;
Fila;TotalFilas-(NumArea-1)*filas;
INDICE(rangos;Fila;1;NumArea))
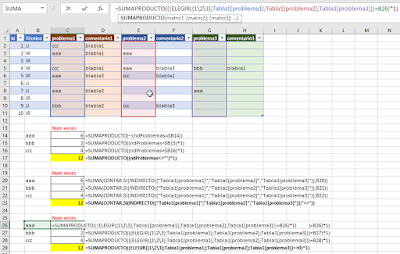
Sobre ese vector construido matricialmente podemos realizar la siguiente operación en C14:
=SUMAPRODUCTO((ndProblemas=$B14)*1)
donde evaluamos los VERDADEROS o las coincidencias del vector (ndProblemas) con el valor de B14, al que multiplicamos por 1 para convertirlo en valor y poder sumarlo...
Igualmente válido (y más 'profesional') sería la alternativa:
=SUMAPRODUCTO(--(ndProblemas=$B14))
esto es, empleando el doble menos.

Luego podremos arrastrar hacia abajo para conocer las coincidencias para B15 y B16.

Una segunda manera de lograr nuestro conteo será empleando la combinación de funciones clásicas como: SUMA, CONTAR.SI o INDIRECTO.
Veamos como... en C20 insertamos:
=SUMA(CONTAR.SI(INDIRECTO({"Tabla1[problema1]";"Tabla1[problema2]";"Tabla1[problema3]"});B20))
/ donde INDIRECTO transforma la matriz de constantes {"Tabla1[problema1]";"Tabla1[problema2]";"Tabla1[problema3]"} en los rangos sobre los que contar.. cosa que hará CONTAR.SI, obteniendo por tanto tres conteos!: {3;2;0} (para mi primer caso).
Finalmente sumaremos esos tres valores devueltos matricialmente con SUMA.

Vemos aquí una solución con un razonamiento de aplicación bastante clásico y fácil de comprender...

Vamos con una tercera alternativa.
En C26 insertamos una anidación de ELEGIR en SUMAPRODUCTO:
=SUMAPRODUCTO(((ELEGIR({1\2\3};Tabla1[problema1];Tabla1[problema2];Tabla1[problema3]))=B26)*1)
Donde la peculiaridad la aporta el uso matricial de ELEGIR que nos permite construir un rango o matriz continuo de tres columnas (en nuestro ejemplo) al llamar a la matriz de constantes {1\2\3}... para una vez montada dicha matriz proceder a compararlo con el valor de la ceda B26 y siguientes...
Si ejecutamos ELEGIR({1\2\3};Tabla1[problema1];Tabla1[problema2];Tabla1[problema3]) de manera separada tendríamos la matriz de 3 columnas por 10 filas:
{"ccc"\0\0;"aaa"\"aaa"\0;0\0\0;"ccc"\"aaa"\"bbb";"aaa"\"ccc"\0;0\0\0;"aaa"\0\"aaa";0\0\0;"bbb"\"ccc"\0;0\0\0}
Tras la comparativa aplicaremos SUMAPRODUCTO para obtener el conteo de coincidencias o VERDADEROS.

Adicionalmente a los cálculos previos, podemos obtener el conteo de celdas vacías en esos rango no adyacentes con alguna de las siguientes fórmulas:
=SUMAPRODUCTO((ndProblemas="")*1) (o también =SUMAPRODUCTO(--(ndProblemas="")))
otra manera
=SUMA(CONTAR.SI(INDIRECTO({"Tabla1[problema1]";"Tabla1[problema2]";"Tabla1[problema3]"});""))
o bien
=SUMAPRODUCTO((ELEGIR({1\2\3};Tabla1[problema1];Tabla1[problema2];Tabla1[problema3])=0)*1)
Algunas de estas funciones se deberán ejecutar, según la versión, matricialmente... esto es, presionando Ctrl+Mayusc+Enter OJO!!.

Como comentario final, vistas algunas de las alternativas, decir que la potencia de las fórmulas descritas está en que los rangos podrían estar incluso en hojas diferentes o ser de tamaños distintos... es decir, potencia en estado puro ;-)