MEDIA GEOMÉTRICA versus MEDIA ARITMÉTICA

Hoy veremos cómo y cuándo aplicar a nuestros cálculos la MEDIA GEOMÉTRICA (la función de Excel MEDIA.GEOM) con sintáxis:
=MEDIA.GEOM(num1;num2;....)

OJO, por que si alguno de los puntos de datos ≤ 0, media devolverá el #NUM! o #VALOR!.
La media geométrica (MEDIA.GEOM) de un conjunto de números estrictamente positivos (X1, X2,…,XN) es el resultado de aplicar la raíz N-ésima del producto de los N elementos.
Lo importante es el cúando emplearla... La misma ayuda de Excel nos da una pista: [sic]puede usar MEDIA.GEOM para calcular la tasa de crecimiento promedio, dado un interés compuesto por tasas variables.[sic].
En definitiva, la media geométrica es útil para calcular medias de porcentajes, tantos por uno, puntuaciones o índices. Con la ventaja de que no ser tan sensible a los valores atípicos o extremos como la media aritmética (PROMEDIO en Excel).

Veamos un ejemplo con unas previsiones de ventas para los siguientes cinco años, con tasas de variación de un año respecto al anterior:

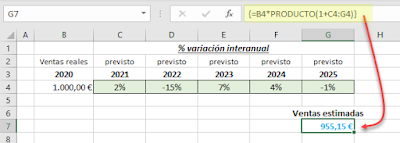
Partimos de unas ventas reales en el 2020 de 1.000 euros, y estimamos unas variaciones para los siguientes años (respecto al anterior) de: 2%, -15%, 7%, 4%, -1%
Esto significaría, haciendo el cálculo manual, que en el 2025 tendríamos unas ventas de:
=1.000 x (1+2%) x (1+15%) x (1+7%) x (1+4%) x (1-1%) = 955,15 euros.

Esto es fácil de conseguir en nuestra hoja de cálculo, bien aplicando la fórmula anterior, o bien empleando alguna forma matricial, por ejemplo en la celda G7:
=B4*PRODUCTO(1+C4:G4) (recuerda ejecutarla matricialmente para mayor seguridad, i.e., presionando Ctrl+Mayus+Enter).

Obteniendo idéntico resultado: 955,15.

Otra cuestión relevante sería conocer cuál es la media para cada uno de esos cinco años de variación interanual... y qué tipo de media deberíamos aplicar (geométrica o aritmética).
Calculemos ambas...
Comenzemos buscando la media geométrica.
En nuestro ejemplo, como se observa, tenemos variaciones negativas, por lo que directamente NO sería posible aplicar la función MEDIA.GEOM (no admite valores negativos o ceros)... pero si reajustamos las variaciones sobre base 100, esto es, sobre los valores acumulados (sumando 1 a cada variación), los valores de cálculo serían:
102%, 85%, 107%, 104% y 99%
donde si podemos aplicar la función... Vemos en F10 la fórmula matricial:
=MEDIA.GEOM(1+C4:G4)-1

Dando como resultado, para nuestro ejemplo, -0,914% de media para cada uno de los cinco años.

'Curiosamente' si aplicamos esta media acumulada para cada uno de los cinco años, en G10 la fórmula matricial:
=B4*(MEDIA.GEOM(1+C4:G4))^5
o también sobre F10
=B4*(1+F10)^5
conseguimos el mismo resultado de 955,15 que ya habíamos logrado con el cálculo manual, año por año... Interesante ;-)
Es decir, con el cálculo de la media geométrica llegamos al mismo resultado equivalente, lo que indica que es una media correcta!.

Repetimos los pasos para la media aritmética (PROMEDIO).
Introducimos en F13 la matricial:
=PROMEDIO(1+C4:G4)-1

Ya podemos comparar con el cálculo de la media geométrica (-0,914%) frente a la media aritmética (-0,600%) ...
Si aplicamos el acumulado para los cinco años en G13 con la matricial:
=B4*(1+PROMEDIO(C4:G4))^5
o también
=B4*(1+F13)^5
resulta un valor de 970,36, valor superior al previo calculado, y algo lejos del resultado exacto.

Esto podría demostrar que la media geométrica resulta más representativa, trabajando con variaciones porcentuales, que la media aritmética.