Conocemos la existencia de los tres métodos de cálculo que Solver nos ofrece:
1-GRG Nonlinear
2-Simplex LP
3-Evolutionary
Los dos primeros son los más frecuentes, y los más ágiles...
pero hoy nos detendremos del método Evolutionary de Solver para Excel.
una gran desventaja es el tiempo que requiere para su resolución, ya que su algoritmo consiste en una búsqueda constante de una mejor solución (que no necesariamente la óptima!!).
Aquí radica la relevancia de este método frente a los otros dos... ya que en ciertos modelos en nuestras hojas, con soluciones múltiples, nos viene muy bien no buscar una única solución óptima, válida en cualquier caso, si no que nos basta la mejor solución posible que se encuentre.
Y en esto consiste nuestro ejercicio de hoy.
Tenemos un listado de once partidas que tenemos que repartir lo más equitativamente entre dos personas de acuerdo al importe de cada partida.
Como siempre en Solver la construcción del modelo en la hoja de cálculo lo es todo...
Debemos habituarnos a construir condiciones sobre la hoja que de otra forma serían complicadas en lal configuración del propio Solver.
En mi modelo he añadido algunas que he considerado pueden ayudar a su resolución (celdas azules).
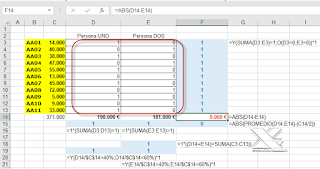
1-celdas F3:E13 con la fórmula:
=Y(SUMA(D3:E3)=1;O(D3=0;E3=0))*1
2-celda D15:
=1*(SUMA(D3:D13)>1)
3-celda E15:
=1*(SUMA(E3:E13)>1)
4-celda E18:
=1*((D14+E14)=SUMA(C3:C13))
5-celda D19:
=Y(D14/$C$14>40%;D14/$C$14<60%)*1
6-celda E19:
=Y(E14/$C$14>40%;E14/$C$14<60%)*1
7-celda F15:
=ABS(PROMEDIO(D14:E14)-(C14/2))
Es muy posible algunas sean redundantes e innecesarias... pero con Solver mejor pecar de exceso.
Nota: observemos como todas las fórmulas (son pruebas lógicas) están multiplicadas por 1 para tener como resultado 0 o 1 (falso o verdadero), con el fin de poder emplearlos fácilmente en la configuración de Solver.
Por otra parte tenemos como celda objetivo a F14:
=ABS(D14-E14)
Ya podemos entrar en Solver y su configuración.
Las restricciones que hemos incorporado en el modelo se basan en esas 'celdas azules' formuladas descritas anteriormente:
1- D19:E19 que tomen valor 1 (esto es, que sean VERDADERO)
2- D15:E15 que tomen valor 1 (esto es, que sean VERDADERO)
3- F3:F13 que tomen valor 1 (esto es, que sean VERDADERO)
4- E18 que tome valor 1 (esto es, que sea VERDADERO)
5- F15>=0 esto es, que la diferencia sea positiva... redundante por que se calcula sobre el valor absoluto.. pero no la vamos a quitar ;-)
y una más, muy importante, al rango a rellenar D3:E13 se le exige sean número binarios, es decir, se completo con ceros y unos
6- D3:E13 = bin
Hemos marcado como celda objetivo la celda F14 que contiene la fórmula:
=ABS(D14-E14)
al que exigimos que se minimice.
D14 contiene la fórmula
=SUMAPRODUCTO($C$3:$C$13;D3:D13)
y E14 la fórmula
=SUMAPRODUCTO($C$3:$C$13;E3:E13)
Como celdas cambiantes o variables el rango D3:E13 (al que hemos exigido sean binarios).
Y por último, indicamos como método de resolución de Solver el método Evolutionary
Importante es tener las opciones del método de resolución definidas...
En este método especialmente relevante es el tiempo de espera, i.e., el tiempo máximo sin mejora.
Lo dejaremos en 30.
Ojo por que tendremos que jugar con este tiempo hasta lograr el equilibrio
Hemos acabado nuestra configuración de Solver... y podríamos lanzarlo o resolverlo ya.
Pero para 'ayudarlo' un poco, y esto es un truco curioso, vamos a completar en las celdas D3:E13 con unos y ceros al azar, para partir de una solución, solución mejorable por supuesto.
Por ejemplo alternando entre las dos personas 0 y 1:
Por supuesto esto es una solución, en sí misma, al reparto que deseamos conseguir, pero ¿es la mejor que podemos encontrar?.
Lo sabremos enseguida al ejecutar Solver.
Fíjate en la barra de estado, en su parte izquierda.. verás algo curioso.
Nos informa de:
Incumbente: mejor solución hasta ahora
Subproblema: número del intento realizado
Solución de prueba: solución intermedia
Celda objetivo: valor de la celda objetivo
Al finalizar el proceso aparece la típica venta de Solver resumiendo qué ha ocurrido.
En la ventana de resolución de este método Evolutionary suele aparecer un texto algo diferente, en nuestro ejemplo:
Solver no puede mejorar la solución actual. Se cumplen todas las restricciones
Leemos lo esperado... hemos llegado a una solución no mejorable.. al menos en los tiempos máximos de espera que le hemos dado
Al aceptar se plasma el resultado en la hoja de cálculo y comprobamos como el reparto no puede ser más equitativo... ambas personas suman casi la misma cantidad... Objetivo conseguido!!
1-GRG Nonlinear
2-Simplex LP
3-Evolutionary
Los dos primeros son los más frecuentes, y los más ágiles...
pero hoy nos detendremos del método Evolutionary de Solver para Excel.
una gran desventaja es el tiempo que requiere para su resolución, ya que su algoritmo consiste en una búsqueda constante de una mejor solución (que no necesariamente la óptima!!).
Aquí radica la relevancia de este método frente a los otros dos... ya que en ciertos modelos en nuestras hojas, con soluciones múltiples, nos viene muy bien no buscar una única solución óptima, válida en cualquier caso, si no que nos basta la mejor solución posible que se encuentre.
Y en esto consiste nuestro ejercicio de hoy.
Tenemos un listado de once partidas que tenemos que repartir lo más equitativamente entre dos personas de acuerdo al importe de cada partida.
Como siempre en Solver la construcción del modelo en la hoja de cálculo lo es todo...
Debemos habituarnos a construir condiciones sobre la hoja que de otra forma serían complicadas en lal configuración del propio Solver.
En mi modelo he añadido algunas que he considerado pueden ayudar a su resolución (celdas azules).
1-celdas F3:E13 con la fórmula:
=Y(SUMA(D3:E3)=1;O(D3=0;E3=0))*1
2-celda D15:
=1*(SUMA(D3:D13)>1)
3-celda E15:
=1*(SUMA(E3:E13)>1)
4-celda E18:
=1*((D14+E14)=SUMA(C3:C13))
5-celda D19:
=Y(D14/$C$14>40%;D14/$C$14<60%)*1
6-celda E19:
=Y(E14/$C$14>40%;E14/$C$14<60%)*1
7-celda F15:
=ABS(PROMEDIO(D14:E14)-(C14/2))
Es muy posible algunas sean redundantes e innecesarias... pero con Solver mejor pecar de exceso.
Nota: observemos como todas las fórmulas (son pruebas lógicas) están multiplicadas por 1 para tener como resultado 0 o 1 (falso o verdadero), con el fin de poder emplearlos fácilmente en la configuración de Solver.
Por otra parte tenemos como celda objetivo a F14:
=ABS(D14-E14)
Ya podemos entrar en Solver y su configuración.
Las restricciones que hemos incorporado en el modelo se basan en esas 'celdas azules' formuladas descritas anteriormente:
1- D19:E19 que tomen valor 1 (esto es, que sean VERDADERO)
2- D15:E15 que tomen valor 1 (esto es, que sean VERDADERO)
3- F3:F13 que tomen valor 1 (esto es, que sean VERDADERO)
4- E18 que tome valor 1 (esto es, que sea VERDADERO)
5- F15>=0 esto es, que la diferencia sea positiva... redundante por que se calcula sobre el valor absoluto.. pero no la vamos a quitar ;-)
y una más, muy importante, al rango a rellenar D3:E13 se le exige sean número binarios, es decir, se completo con ceros y unos
6- D3:E13 = bin
Hemos marcado como celda objetivo la celda F14 que contiene la fórmula:
=ABS(D14-E14)
al que exigimos que se minimice.
D14 contiene la fórmula
=SUMAPRODUCTO($C$3:$C$13;D3:D13)
y E14 la fórmula
=SUMAPRODUCTO($C$3:$C$13;E3:E13)
Como celdas cambiantes o variables el rango D3:E13 (al que hemos exigido sean binarios).
Y por último, indicamos como método de resolución de Solver el método Evolutionary
Importante es tener las opciones del método de resolución definidas...
En este método especialmente relevante es el tiempo de espera, i.e., el tiempo máximo sin mejora.
Lo dejaremos en 30.
Ojo por que tendremos que jugar con este tiempo hasta lograr el equilibrio
Hemos acabado nuestra configuración de Solver... y podríamos lanzarlo o resolverlo ya.
Pero para 'ayudarlo' un poco, y esto es un truco curioso, vamos a completar en las celdas D3:E13 con unos y ceros al azar, para partir de una solución, solución mejorable por supuesto.
Por ejemplo alternando entre las dos personas 0 y 1:
Por supuesto esto es una solución, en sí misma, al reparto que deseamos conseguir, pero ¿es la mejor que podemos encontrar?.
Lo sabremos enseguida al ejecutar Solver.
Fíjate en la barra de estado, en su parte izquierda.. verás algo curioso.
Nos informa de:
Incumbente: mejor solución hasta ahora
Subproblema: número del intento realizado
Solución de prueba: solución intermedia
Celda objetivo: valor de la celda objetivo
Al finalizar el proceso aparece la típica venta de Solver resumiendo qué ha ocurrido.
En la ventana de resolución de este método Evolutionary suele aparecer un texto algo diferente, en nuestro ejemplo:
Solver no puede mejorar la solución actual. Se cumplen todas las restricciones
Leemos lo esperado... hemos llegado a una solución no mejorable.. al menos en los tiempos máximos de espera que le hemos dado
Al aceptar se plasma el resultado en la hoja de cálculo y comprobamos como el reparto no puede ser más equitativo... ambas personas suman casi la misma cantidad... Objetivo conseguido!!







Muy bueno y poco conocido.
ResponderEliminarGracias!