Estudiaremos hoy un herramienta interesante específica del Análisis de datos en Excel, y pensada para la estimación de resultados...
Supongamos tenemos una serie de datos histórica que refleja el 'Coste de mano de obra' de una empresa durante los últimos once meses, con datos del 'número de empleados' por mes, así como de 'horas reales trabajadas':
El objetivo es estimar el dato Coste de mano de obra de diciembre-2018 sabiendo que tendremos 11 empleados contratados que trabajarán un número de 350 horas... y encontrar la ecuación de regresión lineal múltiple.
Coste mano de obra = constante + parámetro1*Num_empleados + parámetro2*Horas_Trabajadas
Para tal fin emplearemos una herramienta contenida en el 'pack' de Análisis de datos (ficha Datos > Análisis)
OJO!, requiere tener el complemento instalado!!.
Dentro de las herramientas de análisis buscaremos la Regresión
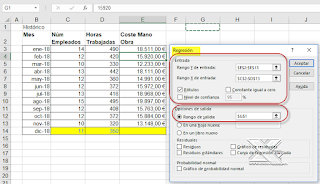
Al abrir la herramienta nos pedirá completar algunos parámetros:
Sección Entrada
1-Rango Y de entrada: E2:E13 que corresponde al rango de celdas con el histórico de Coste de mano obra
2-Rango X de entrada: C2:D13 que corresponde con nuestras dos variables: empleados y horas trabajadas
3-Rótulos: marcado ya que en los rangos anteriores incluimos los encabezados
4-Nivel de confianza: sin marcar por que nos vale el nivel al 95% (o el alfa=0,05)
5-Constante igual a cero: sin marcar por que nos interesa una constante en nuestra futura ecuación
Sección Salida
1-Rango de salida: G1 será la celda superior izquierda del rango destino
No marcaremos ninguna otra opción para no recargar el análisis...
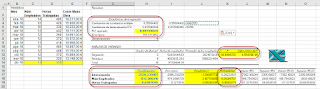
Tras aceptar vemos los siguientes resultados...
De especial relevancia para el análisis e interpretación de nuestra regresión lineal múltiple son los datos marcados en las Estadísticas de la regresión, que paso a resumir:
Coeficiente de correlación múltiple:= 0,95804402
Coeficiente de determinación R^2:= 0,917848345
R^2 ajustado:= 0,897310431
Error típico:= 765,9173652
El cálculo mostrado para el coef de correlación múltiple (R) será la raíz cuadrada del Coeficiente de determinación R^2, y este último viene del cociente entre la 'suma de los cuadrados de la regresión' entre 'la suma de los cuadrados del total'...
Aunque para los casos de regresión lineal múltiple es conveniente fijarse en el R^2 ajustado, ya que este es la medida que define el porcentaje explicado por la varianza de la regresión en relación con la varianza de la variable explicada, esto es, lo mismo que el R^2, pero con una diferencia, y es que el R^2 ajustado tiene en cuenta el tamaño muestral y la inclusión de variables.
Este R^2 ajustado y el R^2 'normal' debe ser un valor entre 0 y 1.. cuanto más próximo a 1 mejor reflejaría una correlación.
Por otra parte es importante que el error típico sea lo más bajo posible.
Otras variables relevantes son dentro de la sección de ANOVA (Análisis de varianza):
F:= 44,69043718
Valor crítico de F:= 4,55476E-05
Este valor nos aporta la significación (si es o no relevante el análisis obtenido); siempre que el valor crítico sea inferior al alfa del estudio (en nuestro caso alfa=0,05 = 1-0,95)
En nuestro caso es netamente inferior a 0,05, con un valor crítico de casi cero; con lo que concluimos que a nivel global es significativo.
De la última sección del análisis nos quedaremos con los coeficientes de la ecuación de regresión:
Intercepción:= -2528,239987 -el valor de la constante de la ecuación buscada
Núm Empleados:= 1513,960316 -el parámetro para la primera variable
Horas Trabajadas:= 0,63819145 -el parámetro para la segunda variable
con esto construimos nuestra ecuación buscada:
Coste mano de obra = -2528,24 + 1513,96*Num_Empleados + 0,64*Horas_trabajadas
ecuación con la que podríamos estimar datos futuros...
Pero para certificar que nuestra ecuación es válida tenemos que fijarnos, al menos, en otro parámetro que nos aportará información sobre la significación local
Estadístico t
Intercepción:= -1,206087721
Núm Empleados:= 3,187709856
Horas Trabajadas:= 0,052624141
y de manera más relevante
Probabilidad
Intercepción:= 0,262239309
Núm Empleados:= 0,01284757 - valores inferiores a alfa (alfa=0,05) serán significativos (Significativa)
Horas Trabajadas:= 0,959321713 - valores inferiores a alfa (alfa=0,05) serán significativos (NO significativa)
En nuestro ejemplo solo la variable 'Num empleados' es significativa!!, así pues, esta lectura nos lleva a la conclusión que podríamos prescindir de ella en el análisis de nuestros datos...
Lanzaremos entonces de nuevo el proceso solo para la variable independiente 'Num empleados' obteniendo los siguientes resultados:
Al hacer el mismo análisis sobre los datos relevantes obtenidos leemos que:
Datos marcados en las Estadísticas de la regresión, que paso a resumir:
Coeficiente de correlación múltiple:= 0,958029179
Coeficiente de determinación R^2:= 0,917819907
R^2 ajustado:= 0,908688786
Error típico:= 722,2387906
Dentro de la sección de ANOVA (Análisis de varianza):
F:= 100,5155735
Valor crítico de F:= 3,50246E-06
que indica la significación a nivel global del estudio.
Finalmente recuperamos los coeficientes de la ecuación de regresión:
Intercepción:= -2559,704918
Núm Empleados:= 1537,442623
con lo que nuestra ecuación buscada será:
Coste mano de obra = -2559.70 + 1537,44*Num_Empleados
y los valores que determinan la significación local:
Estadístico t
Intercepción:= -1,351072511
Núm Empleados:= 10,02574553
y de manera más relevante
Probabilidad
Intercepción:= 0,209655471
Núm Empleados:= 3,50246E-06 - valores inferiores a alfa (alfa=0,05) serán significativos
Que nos indica que en este caso, la variable 'Num empleados' sí es significativa.
En definitiva, tras analizar ambos análisis determinamos que el mejor es el segundo donde correlacionamos únicamente el coste de mano de obra con el número de empleados a través de la ecuación:
Coste mano de obra = -2559.70 + 1537,44*Num_Empleados
sabiendo que si es significativo a nivel global y local, que tiene un R^2 ajustado muy alto y un error típico muy bajo...
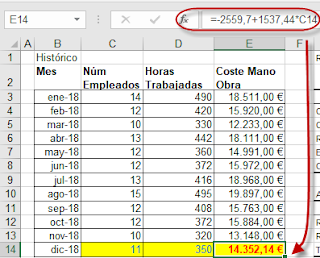
Podemos entonces estimar cuál será el coste de mano de obra en diciembre suponiendo empleemos a 11 trabajadores al 95%, en la celda E14:
=-2559,7+1537,44*C14
Supongamos tenemos una serie de datos histórica que refleja el 'Coste de mano de obra' de una empresa durante los últimos once meses, con datos del 'número de empleados' por mes, así como de 'horas reales trabajadas':
El objetivo es estimar el dato Coste de mano de obra de diciembre-2018 sabiendo que tendremos 11 empleados contratados que trabajarán un número de 350 horas... y encontrar la ecuación de regresión lineal múltiple.
Coste mano de obra = constante + parámetro1*Num_empleados + parámetro2*Horas_Trabajadas
Para tal fin emplearemos una herramienta contenida en el 'pack' de Análisis de datos (ficha Datos > Análisis)
OJO!, requiere tener el complemento instalado!!.
Dentro de las herramientas de análisis buscaremos la Regresión
Al abrir la herramienta nos pedirá completar algunos parámetros:
Sección Entrada
1-Rango Y de entrada: E2:E13 que corresponde al rango de celdas con el histórico de Coste de mano obra
2-Rango X de entrada: C2:D13 que corresponde con nuestras dos variables: empleados y horas trabajadas
3-Rótulos: marcado ya que en los rangos anteriores incluimos los encabezados
4-Nivel de confianza: sin marcar por que nos vale el nivel al 95% (o el alfa=0,05)
5-Constante igual a cero: sin marcar por que nos interesa una constante en nuestra futura ecuación
Sección Salida
1-Rango de salida: G1 será la celda superior izquierda del rango destino
No marcaremos ninguna otra opción para no recargar el análisis...
Tras aceptar vemos los siguientes resultados...
De especial relevancia para el análisis e interpretación de nuestra regresión lineal múltiple son los datos marcados en las Estadísticas de la regresión, que paso a resumir:
Coeficiente de correlación múltiple:= 0,95804402
Coeficiente de determinación R^2:= 0,917848345
R^2 ajustado:= 0,897310431
Error típico:= 765,9173652
El cálculo mostrado para el coef de correlación múltiple (R) será la raíz cuadrada del Coeficiente de determinación R^2, y este último viene del cociente entre la 'suma de los cuadrados de la regresión' entre 'la suma de los cuadrados del total'...
Aunque para los casos de regresión lineal múltiple es conveniente fijarse en el R^2 ajustado, ya que este es la medida que define el porcentaje explicado por la varianza de la regresión en relación con la varianza de la variable explicada, esto es, lo mismo que el R^2, pero con una diferencia, y es que el R^2 ajustado tiene en cuenta el tamaño muestral y la inclusión de variables.
Este R^2 ajustado y el R^2 'normal' debe ser un valor entre 0 y 1.. cuanto más próximo a 1 mejor reflejaría una correlación.
Por otra parte es importante que el error típico sea lo más bajo posible.
Otras variables relevantes son dentro de la sección de ANOVA (Análisis de varianza):
F:= 44,69043718
Valor crítico de F:= 4,55476E-05
Este valor nos aporta la significación (si es o no relevante el análisis obtenido); siempre que el valor crítico sea inferior al alfa del estudio (en nuestro caso alfa=0,05 = 1-0,95)
En nuestro caso es netamente inferior a 0,05, con un valor crítico de casi cero; con lo que concluimos que a nivel global es significativo.
De la última sección del análisis nos quedaremos con los coeficientes de la ecuación de regresión:
Intercepción:= -2528,239987 -el valor de la constante de la ecuación buscada
Núm Empleados:= 1513,960316 -el parámetro para la primera variable
Horas Trabajadas:= 0,63819145 -el parámetro para la segunda variable
con esto construimos nuestra ecuación buscada:
Coste mano de obra = -2528,24 + 1513,96*Num_Empleados + 0,64*Horas_trabajadas
ecuación con la que podríamos estimar datos futuros...
Pero para certificar que nuestra ecuación es válida tenemos que fijarnos, al menos, en otro parámetro que nos aportará información sobre la significación local
Estadístico t
Intercepción:= -1,206087721
Núm Empleados:= 3,187709856
Horas Trabajadas:= 0,052624141
y de manera más relevante
Probabilidad
Intercepción:= 0,262239309
Núm Empleados:= 0,01284757 - valores inferiores a alfa (alfa=0,05) serán significativos (Significativa)
Horas Trabajadas:= 0,959321713 - valores inferiores a alfa (alfa=0,05) serán significativos (NO significativa)
En nuestro ejemplo solo la variable 'Num empleados' es significativa!!, así pues, esta lectura nos lleva a la conclusión que podríamos prescindir de ella en el análisis de nuestros datos...
Lanzaremos entonces de nuevo el proceso solo para la variable independiente 'Num empleados' obteniendo los siguientes resultados:
Al hacer el mismo análisis sobre los datos relevantes obtenidos leemos que:
Datos marcados en las Estadísticas de la regresión, que paso a resumir:
Coeficiente de correlación múltiple:= 0,958029179
Coeficiente de determinación R^2:= 0,917819907
R^2 ajustado:= 0,908688786
Error típico:= 722,2387906
Dentro de la sección de ANOVA (Análisis de varianza):
F:= 100,5155735
Valor crítico de F:= 3,50246E-06
que indica la significación a nivel global del estudio.
Finalmente recuperamos los coeficientes de la ecuación de regresión:
Intercepción:= -2559,704918
Núm Empleados:= 1537,442623
con lo que nuestra ecuación buscada será:
Coste mano de obra = -2559.70 + 1537,44*Num_Empleados
y los valores que determinan la significación local:
Estadístico t
Intercepción:= -1,351072511
Núm Empleados:= 10,02574553
y de manera más relevante
Probabilidad
Intercepción:= 0,209655471
Núm Empleados:= 3,50246E-06 - valores inferiores a alfa (alfa=0,05) serán significativos
Que nos indica que en este caso, la variable 'Num empleados' sí es significativa.
En definitiva, tras analizar ambos análisis determinamos que el mejor es el segundo donde correlacionamos únicamente el coste de mano de obra con el número de empleados a través de la ecuación:
Coste mano de obra = -2559.70 + 1537,44*Num_Empleados
sabiendo que si es significativo a nivel global y local, que tiene un R^2 ajustado muy alto y un error típico muy bajo...
Podemos entonces estimar cuál será el coste de mano de obra en diciembre suponiendo empleemos a 11 trabajadores al 95%, en la celda E14:
=-2559,7+1537,44*C14





Mi versión de Excel no tiene la utilidad de Análisis de Datos. ¿Se podría hacer el ejercicio con fórmulas? Muchas gracias de antemano. Un saludo.
ResponderEliminarHola,
Eliminarel Análisis de datos es un complemento (normalmente preinstalado en todas las versiones)... puedes acceder a la ventana de complementos y activarlo
Saludos
Muchas gracias. Un saludo.
Eliminar