Fractales: El Helecho de Bransley - Excel

Aplicaremos hoy un cálculo recursivo para mostrar uno de los fractales más famosos y sencillos: el Helecho de Barnsley.

Es interesante leer algo más de este gran matemático y de su fractal más famoso en Wikipedia.

Si has leído algo al respecto verás que se trata de aplicar una serie de fórmulas dependiendo de una distribución probabilística que se basa en el siguiente cuadro:

Nuestras cuatro fórmulas serán entonces:
0. El punto original será
x₀ = 0
y₀ = 0

1. Para probabilidades acumuladas entre 0,99 a 1 (probabilidad del 1%)
x_n+1=0
y_n+1=0,16 * y_n

2. Para probabilidades acumuladas entre 0,14 y 0,99 (probabilidad del 85%)
x_n+1=0,85 * x_n + 0,04 * y_n
y_n+1= -0,04 * x_n + 0,85 * y_n+ 1,6

3. Para probabilidades acumuladas entre 0,07 y 0,14 (probabilidad del 7%)
x_n+1=0,2 * x_n – 0,26 * y_n
y_n+1= 0,23 * x_n + 0.22 * y_n+ 1,6

4. Para probabilidades acumuladas inferiores a 0,07 (probabilidad del 7%)
x_n+1=-0,15 * x_n + 0,28 * y_n
y_n+1= 0,26 * x_n + 0,24 * y_n+ 0,44

Así pues construimos nuestro modelo a partir de la función ALEATORIO(), la culal nos permitirá obtener una de la cuatro funciones descritas...

En el rango A3:A6001 insertamos la función:
=ALEATORIO()

En las celdas B2 y C2 insertamos el punto (0,0) inicial con valores no formulados.

Y en B3:B6001 añadimos el componente de la equis de nuestras funciones, así en B3 añadimos para luego arrastrar:
=ELEGIR((A3>0,99)+(A3>0,14)+(A3>0,07)+(A3>0);-0,15*B2+0,28*C2;0,2*B2-0,26*C2;0,85*B2+0,04*C2;0)

Esta primera fórmula nos devuelve el valor recursivo de 'x' sobre las fórmulas descritar por Michael Barnsley.
Con la función ELEGIR a partir de una comparativa con las probabilidades acumuladas comentadas:
(A3>0,99)+(A3>0,14)+(A3>0,07)+(A3>0)
sabremos qué función tenemos que recuperar de entre las cuatro.

De forma similar para el valor de 'y', y por tanto en C3 insertamos para luego arrastrar al rango completo C3:C6001:
=ELEGIR((A3>0,99)+(A3>0,14)+(A3>0,07)+(A3>0);0,26*B2+0,24*C2+0,44;0,23*B2+0,22*C2+1,6;-0,04*B2+0,85*C2+1,6;0,16*C2)

Ambas variables formuladas operan de igual forma con la función ELEGIR, la suma del primer argumento dará un 1,2,3 o 4 según el resultado de ALEATORIO, y así poder recuperar una de las cuatro fórmulas de Barnsley.

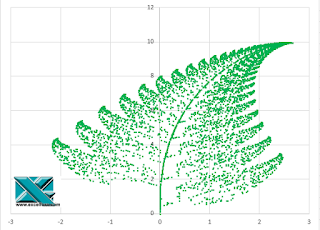
El paso final es simple, construir un gráfico de dispersión normal a partir del rango de datos B1:C6001...
Solo tendrás que ajustar algunos parámetros simples, como por ejemplo bajar el grosor de los marcadores... y si quieres cambiar el color de esos puntos a 'verde helecho' ;-)

Con lo que llegamos al gráfico del inicio.

Interesante aplicación de Excel al mundo de las matemáticas.