Un fantástico 'loco' matemático alemán, Lothar Collatz, enunció en 1937 la que se llamó 'Conjetura de Collatz'... que viene a decir lo siguiente:
Definida una función f(x) para números enteros positivos, siendo:
f(n) = 3n+1 si n es impar
f(n) = n/2 si n es par
Dado un entero m define una secuencia tal que
a(1) = m
y
para i ≥ 1, a(i+1) = f(a(i)).
El problema o conjetura de Collatz nos dice que para cualquier valor inicial m, la secuencia a(i) siempre nos conducirá a 1 !!??
Lo interesante del tema es que la conjetura aún permanece sin demostración!.... aún hoy se sigue buscando un número de partida que rompa con la premisa.
Puedes leer algo más al respecto en la Wikipedia.
Hoy haremos una proyección para los primeros 1.000 números enteros, viendo como se cumple en cada caso... desarrollando un algoritmo con VB para replicar el 'problema de Collatz'
Insertaremos el siguiente procedimiento en un módulo estándar:
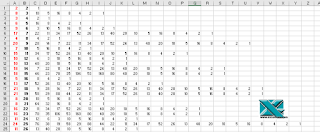
Nuestra macro comienza la secuencia desde la columna B hacia la derecha, por cada fila, i.e., por cada entero, hasta llegar a 1.
Y finalmente coloca en la columna A el número de iteraciones que ha necesitado para alcanzar la unidad.
Como curiosidad si construimos un gráfico de dispersión con los rangos B1:B999 como valores de X y A1:A999 como valores de Y tendríamos este curioso gráfico que nos deja entrever una cierta distribución lógica del número de repeticiones necesarias para alcanzar el 1
No intentes el proceso para números muy grandes por que Excel sobrepasa rápidamente sus especificaciones y entra en un problema de 'sobrepasamiento'.
Definida una función f(x) para números enteros positivos, siendo:
f(n) = 3n+1 si n es impar
f(n) = n/2 si n es par
Dado un entero m define una secuencia tal que
a(1) = m
y
para i ≥ 1, a(i+1) = f(a(i)).
El problema o conjetura de Collatz nos dice que para cualquier valor inicial m, la secuencia a(i) siempre nos conducirá a 1 !!??
Lo interesante del tema es que la conjetura aún permanece sin demostración!.... aún hoy se sigue buscando un número de partida que rompa con la premisa.
Puedes leer algo más al respecto en la Wikipedia.
Hoy haremos una proyección para los primeros 1.000 números enteros, viendo como se cumple en cada caso... desarrollando un algoritmo con VB para replicar el 'problema de Collatz'
Insertaremos el siguiente procedimiento en un módulo estándar:
Sub Collatz_Serie()
Application.ScreenUpdating = False
'recorremos enteros entre 2 y 1000
For i = 2 To 1000
'iniciamos el contador de iteraciones para cada entero
contador = 1
'damos valor a n
n = i
Cells(i - 1, contador + 1).Value = n
'conjetura de Collatz
'inicio del algoritmo
Do
'si es par dividimos por 2
If n Mod 2 = 0 Then
n = n / 2
Else
'si es impar multiplicamos por 3 y sumamos 1
n = 3 * n + 1
End If
'incrementamos el contador
contador = contador + 1
'y devolvemos el resultado a la hoja de cálculo..
Cells(i - 1, contador + 1).Value = n
Loop Until n = 1 'salimos del bucle cuando alcancemos el entero esperado n=1
'llevamos el dato del contador a la columna A
With Cells(i - 1, "A")
.Value = contador
.Font.Bold = True
.Font.Color = vbRed
End With
Next i
Application.ScreenUpdating = True
End SubNuestra macro comienza la secuencia desde la columna B hacia la derecha, por cada fila, i.e., por cada entero, hasta llegar a 1.
Y finalmente coloca en la columna A el número de iteraciones que ha necesitado para alcanzar la unidad.
Como curiosidad si construimos un gráfico de dispersión con los rangos B1:B999 como valores de X y A1:A999 como valores de Y tendríamos este curioso gráfico que nos deja entrever una cierta distribución lógica del número de repeticiones necesarias para alcanzar el 1
No intentes el proceso para números muy grandes por que Excel sobrepasa rápidamente sus especificaciones y entra en un problema de 'sobrepasamiento'.



No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.