Suavización exponencial y el pronóstico de ventas

Tocaremos hoy una herramienta que Excel pone a nuestra disposición para obtener un buen pronóstico o previsión de datos: La Suavización exponencial.

Se trata de aplicar un modelo de alisado exponencial (ver Wikipedia) que se basa en el método de Brown-Holt.

Este modelo de pronóstico precisa tan sólo de tres tipos de datos:
1-el pronóstico del último período (F_t-1),
2-las ventas del último período (A_t-1) y
3-el coeficiente de suavización (alfa, 0<alfa<1).

Responderá a al siguiente fórmula:
F_t=F_t-1+alfa x (A_t-1-F_t-1)


Si bien todo esta formulación la conseguiremos automáticamente a partir de la herramienta de Análisis de datos > Suavización exponencial.
Deberemos tener precaución con los valores dados a 'alfa' (constante de suavización), siendo valores de 0,2 a 0,3 adecuadas. Estos valores indican que el pronóstico actual debe ajustarse entre un 20 % y un 30 % del error en el pronóstico anterior.
Las constantes mayores generan una respuesta más rápida, pero pueden producir proyecciones erróneas. Las constantes más pequeñas pueden dar como resultado retrasos prolongados en los valores pronosticados.

OJO!!, el coeficiente de suavización, en la herramienta Suavización exponencial, responde al complementario empleado en la formulación de Método descrito, esto es, el 'coeficiente de suavización' es igual a (1-alfa) !!

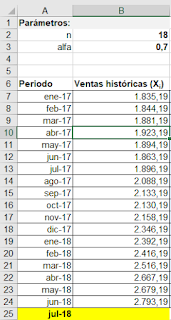
Partiremos de los siguientes datos de ventas:

Accederemos ahora a la ficha Datos > grupo Análisis > botón Análisis de datos y buscaremos la herramienta 'Suavización Exponencial'

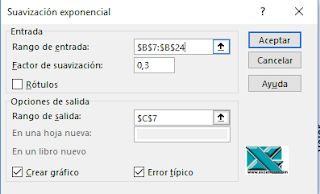
Al abrir la herramienta configuraremos los datos solicitados...

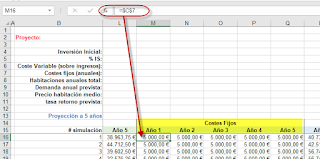
Completamos el Rango de entrada con el rango de celdas donde estén los datos históricos, en mi ejemplo, rango $B$7:$B$24
Como Factor de suavización indicaremos 0,3 (y así nuestro alfa será 1-0,3=0,7).

Como opciones de salida indicaremos la celda superior izquierda del rango destino, por ejemplo C7 y terminamos marcando las dos últimas opciones (de manera voluntaria) para mostrar:
1-Crear Gráfico
2-Error típico

El resultado:

Si comparamos el resultado obtenido en las celdas C7:D24 (a partir de la herramienta de 'Suavización exponencial') con el rango de celdas E7:E24 donde he aplicado las fórmulas:
=+E7+$B$3*(B7-E7)
veremos que es el mismo resultado...

Si hiciéramos alfa=1 el pronóstico o previsión obtenido coincidiría con los datos reales.

En general, podemos decir que este modelo de pronóstico de suavización exponencial simple es óptimo para patrones de ventas aleatorios o igualados, donde queremos eliminar el impacto de los elementos 'irregulares' históricos mediante un enfoque en períodos de ventas recientes.

Sin duda hay mejores, y más ajustados, métodos de previsión... ;-)

Seguir leyendo...

VBA: Conjetura de Collatz y Excel

Un fantástico 'loco' matemático alemán, Lothar Collatz, enunció en 1937 la que se llamó 'Conjetura de Collatz'... que viene a decir lo siguiente:
Definida una función f(x) para números enteros positivos, siendo:
f(n) = 3n+1 si n es impar
f(n) = n/2 si n es par

Dado un entero m define una secuencia tal que
a(1) = m
y
para i ≥ 1, a(i+1) = f(a(i)).
El problema o conjetura de Collatz nos dice que para cualquier valor inicial m, la secuencia a(i) siempre nos conducirá a 1 !!??

Lo interesante del tema es que la conjetura aún permanece sin demostración!.... aún hoy se sigue buscando un número de partida que rompa con la premisa.

Puedes leer algo más al respecto en la Wikipedia.

Hoy haremos una proyección para los primeros 1.000 números enteros, viendo como se cumple en cada caso... desarrollando un algoritmo con VB para replicar el 'problema de Collatz'

Insertaremos el siguiente procedimiento en un módulo estándar:

Sub Collatz_Serie()
Application.ScreenUpdating = False
'recorremos enteros entre 2 y 1000
For i = 2 To 1000
    'iniciamos el contador de iteraciones para cada entero
    contador = 1
    'damos valor a n
    n = i
    Cells(i - 1, contador + 1).Value = n
    'conjetura de Collatz
    'inicio del algoritmo
    Do
        'si es par dividimos por 2
        If n Mod 2 = 0 Then
            n = n / 2
        Else
        'si es impar multiplicamos por 3 y sumamos 1
            n = 3 * n + 1
        End If
        'incrementamos el contador
        contador = contador + 1
        'y devolvemos el resultado a la hoja de cálculo..
        Cells(i - 1, contador + 1).Value = n
    Loop Until n = 1    'salimos del bucle cuando alcancemos el entero esperado n=1
    
    'llevamos el dato del contador a la columna A
    With Cells(i - 1, "A")
        .Value = contador
        .Font.Bold = True
        .Font.Color = vbRed
    End With
Next i
Application.ScreenUpdating = True
End Sub

Nuestra macro comienza la secuencia desde la columna B hacia la derecha, por cada fila, i.e., por cada entero, hasta llegar a 1.
Y finalmente coloca en la columna A el número de iteraciones que ha necesitado para alcanzar la unidad.

Como curiosidad si construimos un gráfico de dispersión con los rangos B1:B999 como valores de X y A1:A999 como valores de Y tendríamos este curioso gráfico que nos deja entrever una cierta distribución lógica del número de repeticiones necesarias para alcanzar el 1

No intentes el proceso para números muy grandes por que Excel sobrepasa rápidamente sus especificaciones y entra en un problema de 'sobrepasamiento'.

Seguir leyendo...

Calculadora Horas Anuales Trabajadas

Seguro te has preguntando muchas veces cuántas horas trabajas al año y si cumples con lo establecido con el convenio que tengas...
Hoy explicaremos como construir una calculadora de horas anuales trabajadas.

Necesitaremos pocas cosas:
1-Tabla con los 14 festivos anuales (lo que tengas en tu convenio reconocidos).
2-Tabla con los 365/366 días del año.
3-Tabla con el número de horas a trabajar por semanas.

haz clic en la imagen

Para el ejemplo tomaré los 14 festivos anuales de Madrid para el 2018.
En una Tabla que llamaré: 'TblFestivos'

Una segunda tabla, que llamaré 'TblTipos', que recogerá la distribución por semanas de las horas trabajadas por cada día (lunes, martes, etc.), según semanas:

Esta tabla es fundamental para nuestra calculadora.
Por lo que debemos verificar algunos puntos:
1- el primer campo 'Desde' debe estar ordenado en sentido ascendente
2- NO es posible solapar fechas en los distintos periodos definidos (i.e., las fechas deben ser un continuo entre intervalos).

La tercera y última tabla nos determinará día por día, de todo el año, cuantas horas hemos trabajado.
Llamaremos a la tabla 'Tbl_2018'.

Comenzaremos listando la serie de fechas desde el 1/1/2018 hasta el 31/12/2018 en el campo 'Días'.
Este campo no tiene fórmula alguna...

El resto de campos se componen de fórmulas diferentes que aportan algo más de información.

Campo 'Día_semana':
insertamos la fórmula:
=ELEGIR(DIASEM([@Dias];2);"lun";"mar";"mie";"jue";"vie";"sab";"dom")
que nos permite convertir en texto el día de la semana para los 365 días del año.

Este campo se empleará posteriormente para localizar las horas de la semana en la 'TblTipos'.

Campo 'Tipo Jornada':
con la fórmula:
=BUSCARV([@Dias];TblTipos[[#Todo];[Desde]:[Tipo]];3;1)

que nos retornará, de manera informativa, a qué tipo de semana corresponde cada día del año a partir de la 'TblTipos'.

Campo 'Lab/No lab':
con la fórmula:
=SI(O(DIASEM([@Dias];2)>=6;NO(ESERROR(BUSCARV([@Dias];TblFestivos[Festivos];1;0))));"No laborable";"laborable")
con esta fórmula condicional verificamos los dos casos en que un día del año es 'no laborable', o bien que sea sábado o domingo:
DIASEM([@Dias];2)>=6
o bien que esté entre los 14 festivos de la tabla 'TblFestivos'
NO(ESERROR(BUSCARV([@Dias];TblFestivos[Festivos];1;0)))

si se cumple alguna de las dos condiciones el día será 'No laborable', en caso contrario 'laborable'.

Finalmente, el último campo 'Horas', con el que asignaremos las horas determinadas para cada día del año.
Insertamos la fórmula:
=SI([@[Lab/No Lab]]="laborable";SUMAR.SI.CONJUNTO(INDIRECTO("TblTipos["&[@[Día_Semana]]&"]");TblTipos[Desde];"<="&[@Dias];TblTipos[Hasta];">="&[@Dias]);0)

Donde condicionamos que si el día fuera 'laborable' recuperaríamos, según fechas y qué día de la semana fuera, el número de horas correspondiente... en cualquier otro caso devolvemos cero horas trabajadas.

Como se observa para recuperar las horas del día a partir de la 'TblTipos' empleamos la función SUMAR.SI.CONJUNTO, ya que se dan las condiciones necesarias:
1- el dato a recuperar es numérico (se puede 'sumar')
2- NO se solapan fechas en los distintos periodos definidos.

Por otra parte el rango a sumar se genera con la función INDIRECTO, que nos aporta el dinamismo necesario para recuperar el dato de una columna u otra...

Solo nos queda sumar el campo de las 'Horas'.
Así en la celda F1 añadimos:
=SUMA(Tbl_2018[Horas])

dando en mi ejemplo un total de 1.764 horas al año trabajadas..
Si se compara con el convenio de donde se han tomado los datos, que indica que el máximo de horas es de 1.765 horas, vemos que se ajusta perfectamente a un calendario de una persona a jornada completa.

Otro caso sería si tuviéramos jornadas parciales ;-)

Salvo opinión en contra de algún experto laboralista, esta calculadora nos permitirá saber si cumplimos o no con la legislación laboral actual.

Espero te sirva.

Seguir leyendo...

Excel y la Maquina de Galton

Recientemente, leyendo el blog del maestro Adolfo Aparicio encontré un post sobre la máquina de Galton, donde desarrollaba mediante macros el experimento de Francis Galton.

Me pareció interesante replicar mediante funciones el comportamiento de esta caja de Galton (ver Wikipedia)

La idea es demostrar como un comportamiento aleatorio sobre la posibilidad de tomar dos caminos conduce a una estructura de campana, tendente a la forma de una campana de Gauss o de una distribución normal.

haz clic en la imagen

Inicialmente generaremos una estructura de pirámide de 11 niveles, comenzando en la cúspide de esta, celda L4 con la fórmula:
=ALEATORIO.ENTRE(0;1)
esta función nos aporta el componente de azar necesario...

Desde de esa celda L4, siguiendo la pendiente izquierda, celdas:
$K$5,$J$6,$I$7,$H$8,$G$9,$F$10,$E$11,$D$12,$C$13 y $B$14
añadimos la fórmula:
=SI(L4=0;ALEATORIO.ENTRE(0;1);"")
es decir, si la celda anterior fuera 0 generamos un nuevo aleatorio 0-1

Desde la celda L4 y siguiendo la pendiente derecha, celda:
$M$5,$N$6,$O$7,$P$8,$Q$9,$R$10,$S$11,$T$12,$U$13 y $V$14
añadimos la fórmula:
=SI(L4=1;ALEATORIO.ENTRE(0;1);"")
es decir, si la celda anterior fuera 1 generamos un nuevo aleatorio 0-1

Completamos el interior de nuestra pirámide aleatoria.
En las celdas alternas:
$L$6,
$K$7,$M$7,
$J$8,$L$8,$N$8,
$I$9,$K$9,$M$9,$O$9,
$H$10,$J$10,$L$10,$N$10,$P$10,
$G$11,$I$11,$K$11,$M$11,$O$11,$Q$11,
$F$12,$H$12,$J$12,$L$12,$N$12,$P$12,$R$12,
$E$13,$G$13,$I$13,$K$13,$M$13,$O$13,$Q$13,$S$13,
$D$14,$F$14,$H$14,$J$14,$L$14,$N$14,$P$14,$R$14,$T$14
con la fórmula en L6:
=SI(O(K5=1;M5=0);ALEATORIO.ENTRE(0;1);"")

Ahora vamos a convertir los 0 y los 1 resultantes en una bolita roja que simula el camino hasta la base.

Seleccionamos el rango $B$4:$V$14 y aplicamos un formato condicional tipo Conjunto de iconos de tres bolas con la siguiente configuración:
+presionamos el botón de 'Invertir criterio de ordenación'
+marcamos la opción para 'Mostrar el icono únicamente' (no mostrar el valor de la celda)
+cambiar a tipo número ambos tramos y asignarles valoro cero en los dos casos

En el siguiente paso obtendremos el dato acumulado de llegadas de las 'bolitas' a cada punto de la base de la pirámide.
Para ello tendremos que cambiar las opciones de Excel respecto al cálculo (a Manual) y las opciones de iteración.
Si accedemos a la ficha Archivo > Opciones de Excel> menú Fórmulas en la primera sección de Opciones de cálculo configuramos:
1-Cálculo de libro: Manual
2-Habilitar cálculo iterativo: marcado
3-Iteraciones máximas: 1

Tras aceptar, podremos incorporar la fórmula que nos permite acumular llegadas...
En las celdas B17,D17,F17,H17,J17,L17,N17,P17,R17,T17 y V17 añadimos la fórmula:
=SI(B14<>"";B17+1;B17)
que nos permite autosumar a la cantidad existente esas celdas, las nuevas llegadas de las bolitas a la base...

Finalmente seleccionando las celdas anteriores de la fila 17 podemos insertar un gráfico de líneas, con la propiedad de línea suavizada para mejorar su aspecto.

Y estamos listos para comprobar la teoría de Francis Galton... puedes empezar a presionar la tecla de función F9 para recalcular el libro de trabajo.
Comprobaremos que según aumentamos el número de simulaciones, el gráfico toma apariencia de una distribución normal, i.e., concentro en los puntos interiores la mayoría de las llegadas...

En mi ejemplo, con unas 7.000 simulaciones, el aspecto es el siguiente:

Seguir leyendo...

Modelo de Montecarlo sobre un proyecto de inversión

En la entrada anterior del Blog hablamos de qué era y como operaba el Método de Montecarlo.
Hoy la daremos un uso más financiero, usándolo para analizar un proyecto de inversión...
en el ejemplo supondremos vamos a invertir en un pequeño hotel rural... y vamos a analizar nuestra inversión a cinco años.

Nuestros datos relevantes (y muy simplificados) son los siguientes:

A continuación desplegamos algunos tramos calculados para los cinco años de estudio:
+Ingresos
+Costes Variables
+Costes Fijos
+RDI (Resultados después de impuestos)
+Flujos de efectivos generados

Lanzaremos 10.000 simulaciones para nuestro proyecto (recuerda siempre que a mayor número de simulaciones más certeza con el resultado).

Nuestro primer bloque servirá para calcular los ingresos esperados de los cinco años.
Asi en el rango C16:G10015 añadimos la fórmula:
=$C$8*$C$10*ALEATORIO.ENTRE(45;75)/100

fórmula que contiene el componente de aleatoriedad necesario para el correcto funcionamiento de este modelo de Montecarlo

En el segundo bloque calcularemos los Costes variables que, de acuerdo a nuestras hipótesis serán del 35% de los ingresos.
Así pues, en el rango H16:L10015 añadimos la fórmula:
=C16*$C$6

En el tercer bloque trabajaremos sobre los Costes Fijos.
En el rango M16:Q10015 añadimos la fórmula/vínculo:
=$C$7
que recupera los costes fijos anuales estimados.

Otro bloque nos servirá para obtener el dato calculado del Resultado de la empresa después de impuestos.
En el rango R16:V10015 añadimos:
=(C16-H16-M16)*(1-$C$5)

esto es, (ingresos-costes variables-costes fijos)x(1-tasa Impuesto)

Llegamos al paso final.
Proyectamos los flujos de tesorería esperados para los cinco años, contando el desembolso inicial de la inversión, que según nuestros datos de partida es de 200.000,00 euros.
Los flujos de los cinco años corresponderán a los Resultados (RDI) de esos años.
En el rango W16:W10015 añadimos la fórmula/vínculo:
=-$C$4
A continuación seleccionamos X16:AB10015 y en X16 añadimos
=R16
y presionamos Ctrl+Enter

Solo nos queda el cálculo del Valor Actual Neto (función VNA en Excel).
OJO!! para el cálculo del VAN hay que usar la función VNA de los flujos positivos más la celda del desembolso inicial.
Por tanto en el rango AC16:AC10015 añadimos:
=VNA($C$11;X16:AB16)+W16

Y finalmente para representar el modelo, y obtener un resultado global, aplicamos un PROMEDIO corrido sobre esos VAN calculados...
En AD16:AD1015 añadimos
=PROMEDIO($AC$16:AC16)

Para la muestra gráfica de hacia donde tiende nuestro VAN, para nuestro proyecto, creamos un gráfico de dispersión.
Seleccionamos nuestro numeral de 10.000 celdas (rango B16:B10015) y también seleccionamos este último rango de promedio corrido (rango AD16:AD10015) e insertamos un gráfico de dispersión:

El gráfico muestra la estabilización hacia un VAN del proyecto cercano a los 12.000 euros... lo que indica que sería nuestro VAN más probable, de acuerdo al modelo de Montecarlo.

Seguir leyendo...

El método de Montecarlo en Excel

Trataremos hoy el tan extendido Método de Montecarlo.
La esencia del método es demostrar como mediante simulaciones tendentes al infinito podemos aproximar una solución a un modelo de cualquier tipo.

En el ejemplo de hoy calcularemos, al hilo de la entrada anterior, la integral definida de una función:
f(x)=2x²
para el intervalo entre 1 y 3.

Para ello comenzaremos a trabajar sobre un rango alto de celdas, en concreto 20.000.
Así pues nos aprovecharemos de la función ALEATORIO() con la que conseguiremos una serie de números distribuidos uniformemente entre 1 y 3.
Excel genera estos aleatorios a partir del algoritmo Mersenne Twister.

En nuestro ejemplo en el rango A9:A20008 insertamos:
=ALEATORIO.ENTRE(1;2)+ALEATORIO()

Por otra parte, empleando estos valores como las x de nuestra función nos permite, en el rango B9:B20008, incluir la fórmula:
=2*POTENCIA(A9;2)

haz clic en la imagen

Para realizar el estudio comparativo generamos una nueva serie aleatoria en el rango C9:C20008 con la fórmula:
=ALEATORIO.ENTRE(0;17)+ALEATORIO()
que devolverá un valor entre 0 y 18, valores entre los que se puede mover nuestra función a estudio.

En último termino comparamos estos valores aleatorios entre 0 y 18 con los obtenidos con nuestra función, y en D9:D20008 insertamos el condicional:
=SI(C9<=B9;C9;0)
que nos dirá cuantos de los puntos distribuidos en el rectángulo entre 1-3 y 0-18 caen por debajo de la línea de nuestra ecuación
f(x)=2x²

Si llevamos estas series a un gráfico de dispersión tendríamos:

Al conocer el número de puntos por debajo de la línea de nuestra función, podemos extrapolar la proporción del área total del rectángulo general (1-3 y 0-18) que correspondería precisamente con el área buscada, esto es, con el cálculo de la integral definida.

Mediante un sencillo cálculo:
=CONTAR.SI(D9:D20008;">0")
conoceremos el número de puntos por debajo de la línea, dentro del área a calcular.
Como sabemos el total de puntos del estudio: 20000
la proporción es fácil de calcular dividiendo uno entro otro...

Esta proporción la multiplicaremos por el área total del rectángulo general (base x altura): (3-1)x(18-0) = 36
Llegando a la integral definida entre 1 y 3 de la función...

haz clic en la imagen

El valor obtenido se aproximará bastante a esos 17,333 conseguido con el cálculo integral...

Recuerda que a mayor número de simulaciones más aproximado será el valor conseguido!!

Seguir leyendo...

Cálculo de Integral definida de Riemann

Hablaremos hoy de un método de cálculo para integrales definidas: Integral de Riemann.
Método de cálculo para integrales definidas, a partir del cual se desarrollaron otros procesos más ajustados (Integral de Lebesgue, por ejemplo).

Obviamente me centraré en la aplicación del método de cálculo empleando Excel. Otras disquisiciones se quedan para los expertos en la materia.
Puedes leer algo más en Wikipedia.

La idea general del cálculo que veremos es obtener el valor de la integral definida por aproximación, forma simple de definir la integral de una función sobre un intervalo como el área localizada bajo la curva de la función.
Y para obtener esa aproximación al área encerrada por debajo de una curva, la dividiremos en rectángulos como indica la figura siguiente.

El área de cada rectángulo, será el producto de la función en ese punto por el ancho del intervalo, como base del rectángulo...
Es importante saber que a mayor número de divisiones de nuestra función, en rectángulos de base menor, la aproximación de nuestro cálculo será mejor.

La idea es que al tender al infinito en la división de esta función en rectángulo por debajo de la función, llegaremos con precisión al área de la función para ese intervalo... es decir al cálculo de la integral definida.

Pondremos como ejemplo de función la parábola:
f(x)=2x²
para el intervalo entre 1 y 3.

Y como primera aproximación dividiremos en 20 tramos nuestra función.

Como primer paso dividiremos en 20 intervalos iguales nuestra función, con la fórmula en el rango B8:B28.
Introducimos en B8 como valor fijo:
1 y en particular en B9 insertamos
=B8+($C$4-$C$3)/$C$5

como se comprueba la operación simplemente responde a una sencilla división de la longitud del intervalo (entre 1 y 3) entre las 20 partes indicadas...

El siguiente paso consiste en saber qué altura tendrá el rectángulo para cada punto anterior...
Lo cual es sencillo de calcular, solo necesitamos aplicar nuestra función
f(x)=2x²
en esos puntos.
Así en el rango de celdas C8:C28 añadimos la fórmula:
=2*POTENCIA(B8;2)

Sabiendo la altura para cada intervalo en cada punto, ya podemos calcular el área de ese rectangulo como:
área =base x altura

sabiendo que la base es la longitud en que dividimos el intervalo entre 1 y 3.

Por tanto, en el rango D8:D28 añadimos la fórmula:
=C8*($C$4-$C$3)/$C$5

Finalmente solo nos queda sumar las diferentes áreas.. para ello es frecuente sumar nuestras áeas por doble partida (desdel punto 0 y desde el punto 1:
En la imagen vemos esa sumas, donde en la celda F2 sumamos: =SUMA(D8:D27)
y en la celda F3: =SUMA(D9:D28)
Promediando y llegando al resultado final en F4 como: =PROMEDIO(F2:F3)

Por tanto, para el intervalo entre 1 y 3, la integral definida de la función
f(x)=2x²
nos lleva a un valor aproximado de 17,34

De hecho si tiramos de cálculo integral, la integral de
f(x)=2x²
es
f(x)=2/3 x³
si damos valor a f(x) para 1 y para 3 serán: 0,67 y 18, y por diferencias:= 18 - 0,67 = 17,33
muy próximo al dato calculado mediante el método de Riemann anterior...

Seguir leyendo...

VBA: Recorrer solo los elementos filtrado de una tabla

Tiempo atrás publiqué un post donde exponía como copiar y pegar únicamente los registros filtrados de una tabla...

Hoy veremos una variante, aprenderemos a recorrer esos elementos filtrados y visibles de una tabla.

Partiremos de una tabla con varios campos a la cual hemos aplicado un filtro cualquiera, por ejemplo, por el país España:

Comprobamos en la imagen que las filas visibles son: 2, 6, 10, 14 y 18

Veremos dos procedimientos muy similares...
Uno primero empleando la propiedad de los rangos
.SpecialCells(xlCellTypeVisible)
y una segunda de la propiedad
.EntireRow.Hidden

Insertaremos el siguiente procedimiento en un módulo estándar:

Sub LoopSpecialTypeVisible()
Dim celda As Range, rng As Range
'definimos el rango a recorrer.. que será un campo cualquiera de la tabla
Set rng = Range("TblDatos[campo3]")
'recorremos ese rango.. pero solo aquellas celdas visibles!!
For Each celda In rng.SpecialCells(xlCellTypeVisible)
    'llevamos la dirección de la celda a la Ventana de inmediato
    Debug.Print celda.Address
Next celda

End Sub

Si lanzamos el procedimiento, en la Ventana de inmediato, veremos:
$C$2
$C$6
$C$10
$C$14
$C$18

Una segunda manera la podemos ver en este procedimiento de en un módulo estándar:

Sub LoopSpecialHidden()
Dim celda As Range, rng As Range
'definimos el rango a recorrer.. que será un campo cualquiera de la tabla
Set rng = Range("TblDatos[campo3]")
'recorremos ese rango.. pero solo aquellas celdas visibles!!
For Each celda In rng
    'verificamos si la fila está mostrada (no oculta)
    If celda.EntireRow.Hidden = False Then
        'llevamos la dirección de la celda a la Ventana de inmediato
        Debug.Print celda.Address
    End If
Next celda

End Sub

LLegando al mismo resultado...

OJO!!, por que ambas maneras emplean una propiedad de visibilidad, lo que implica que si 'ocultamos' (no solo filtramos) una fila, ésta no aparecerá en nuestros listados.

Seguir leyendo...