Algo que todos recordamos de la escuela, pero que nunca nos hemos parado a darle la importancia que merece: Teorema de Pitágoras (de Samos).
Que dice: En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
En el post de hoy mostraremos una explicación geométrica de este teorema, para lo cual emplearemos las Formas de Excel
Comprobaremos de manera casi perfecta como se verifica este teorema.
La idea es construir un cuadrado perfecto 'exterior' con cuatro triángulos rectángulos idénticos, dejando en su parte interior un nuevo cuadrado 'menor', generado a partir de las hipotenusas de los cuatro triángulos.. tal como vemos en la imagen:
Para mostrar esta representación, los valores o medidas tomados son:
c1:= lado 1 (cateto 1 o lado corto del triángulo): 3 cm
c2:= lado 2 (cateto 2 o lado largo del triángulo): 4 cm
h := hipotenusa: 5 cm
Dimensiones que verifican el teorema (32+42=52)
La explicación y demostración visual reside en que el área del cuadrado perfecto exterior, de lado c1 + c2, y por tanto área:
(c1 + c2)2
coincide con la suma de las área de los cuatro triángulos rectángulos más el cuadrado menor de lado h:
h2 + 4 x (c1 x c2) / 2
de donde se consigue:
(c1 + c2)2 = 4 x (c1 x c2/2) + h2
c12 + (2 x c1 x c2) + c22 = (2 x c1 x c2) + h2
c12 + c22 = h2
Demostrando así el famoso teorema.
En cuanto a Excel, cómo construimos nuestra composición.
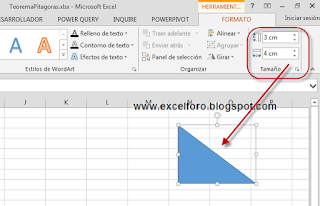
En primer lugar insertamos un triángulo rectángulo:
Una vez insertado, desde su barra de herramientas y su pestaña de Formato accedemos al grupo Tamaño donde cambiamos las propiedades de Alto (=3 cm) y Ancho (=4 cm)
Duplicamos hasta tener cuatro triángulos iguales (si queremos podemos cambiarles el color de relleno)
Intentamos colocarlos de la siguiente manera:
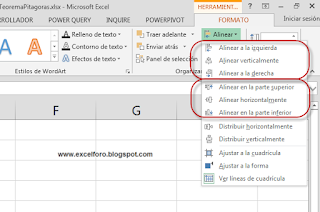
Lo conseguiremos girando/rotando y ayudándonos de la herramienta de Alinear Objetos, dentro de la Barra de herramientas de las Formas > pestaña Formato > grupo Organizar > botón Alinear:
Una vez conseguido el ajuste más perfecto que podamos entre los distintos ángulos, insertaremos una nueva forma: Un Rectángulo
Al que daremos dimensiones de 5 cm de Alto y Ancho.
Ya podemos girarlo y moverlo hasta el hueco formado por nuestros cuatro triángulos (ver imagen inicial)... comprobaremos como encaja en ese área, demostrando por tanto el teorema.
Para ver otras demostraciones y leer algo más al respecto ir a Wikipedia
Que dice: En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
En el post de hoy mostraremos una explicación geométrica de este teorema, para lo cual emplearemos las Formas de Excel
Comprobaremos de manera casi perfecta como se verifica este teorema.
La idea es construir un cuadrado perfecto 'exterior' con cuatro triángulos rectángulos idénticos, dejando en su parte interior un nuevo cuadrado 'menor', generado a partir de las hipotenusas de los cuatro triángulos.. tal como vemos en la imagen:
Para mostrar esta representación, los valores o medidas tomados son:
c1:= lado 1 (cateto 1 o lado corto del triángulo): 3 cm
c2:= lado 2 (cateto 2 o lado largo del triángulo): 4 cm
h := hipotenusa: 5 cm
Dimensiones que verifican el teorema (32+42=52)
La explicación y demostración visual reside en que el área del cuadrado perfecto exterior, de lado c1 + c2, y por tanto área:
(c1 + c2)2
coincide con la suma de las área de los cuatro triángulos rectángulos más el cuadrado menor de lado h:
h2 + 4 x (c1 x c2) / 2
de donde se consigue:
(c1 + c2)2 = 4 x (c1 x c2/2) + h2
c12 + (2 x c1 x c2) + c22 = (2 x c1 x c2) + h2
c12 + c22 = h2
Demostrando así el famoso teorema.
En cuanto a Excel, cómo construimos nuestra composición.
En primer lugar insertamos un triángulo rectángulo:
Una vez insertado, desde su barra de herramientas y su pestaña de Formato accedemos al grupo Tamaño donde cambiamos las propiedades de Alto (=3 cm) y Ancho (=4 cm)
Duplicamos hasta tener cuatro triángulos iguales (si queremos podemos cambiarles el color de relleno)
Intentamos colocarlos de la siguiente manera:
Lo conseguiremos girando/rotando y ayudándonos de la herramienta de Alinear Objetos, dentro de la Barra de herramientas de las Formas > pestaña Formato > grupo Organizar > botón Alinear:
Una vez conseguido el ajuste más perfecto que podamos entre los distintos ángulos, insertaremos una nueva forma: Un Rectángulo
Al que daremos dimensiones de 5 cm de Alto y Ancho.
Ya podemos girarlo y moverlo hasta el hueco formado por nuestros cuatro triángulos (ver imagen inicial)... comprobaremos como encaja en ese área, demostrando por tanto el teorema.
Para ver otras demostraciones y leer algo más al respecto ir a Wikipedia






No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.