Aprenderemos hoy a construir un gráfico de un polígono de hasta 20 lados, empleando el tipo de gráfico Radial.
En primer lugar, a modo didáctico, recordaremos los nombres de los diferentes polígonos... (leer algo más en wikipedia):
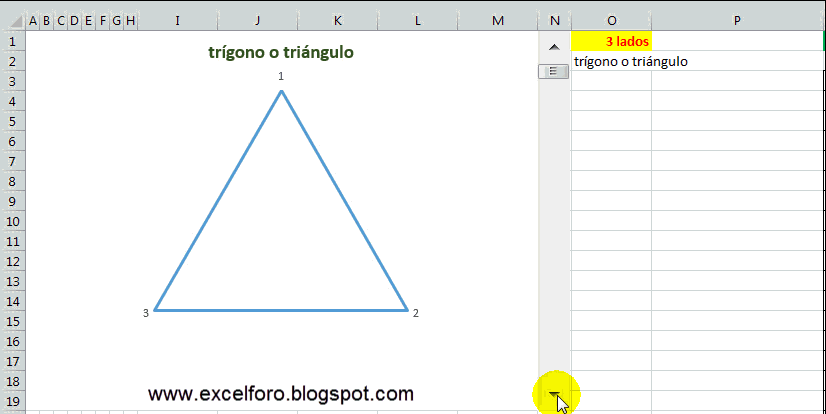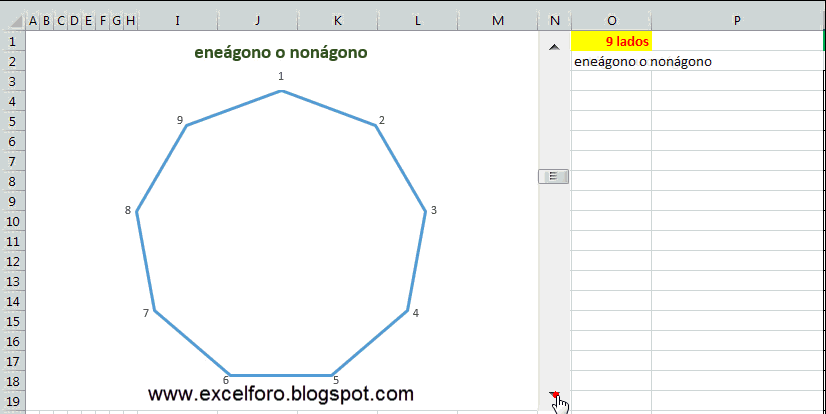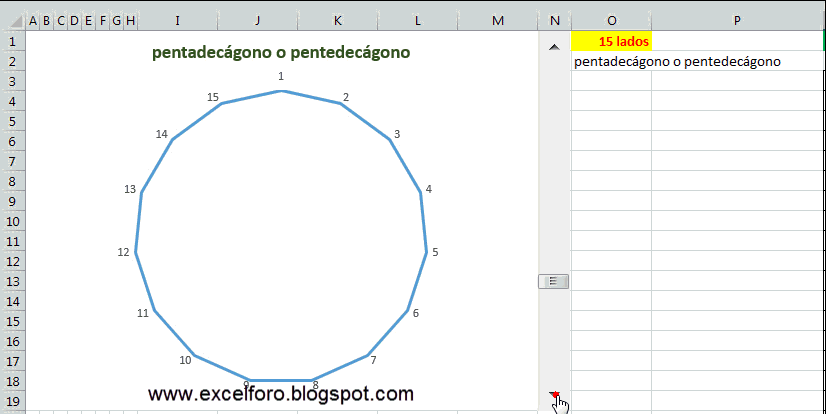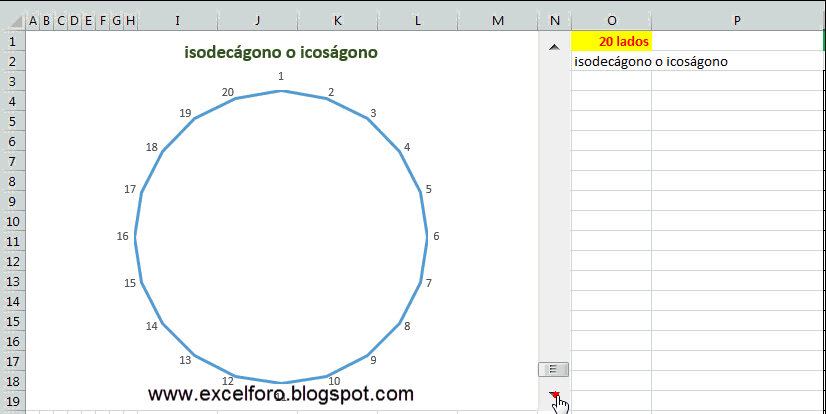
El objetivo es lograr lo siguiente:
Para la construcción en primer lugar dispondremos en un rango de una fila un mismo valor repetido, en mi caso en el rango T1:AM1 dispuse el valor 2 repetido veinte veces....
En segundo lugar seleccionando ese rango insertamos un gráfico tipo Radial.
A continuación eliminamos la etiqueta del eje radial y las líneas de división principal.
Un paso después crearemos el siguiente Nombre Definido:
lados =DESREF(Radial!$T$1;;;1;Radial!$O$1)
que tomará un número determinado de valores según se indique en la celda O1 (que más adelante indentificaremos).
En un paso posterior seleccionamos accedemos a la opción Selección de datos, y Editamos la Serie representada.
Incluimos en esta serie el Nombre definido anterior:
Añadimos ahora una Barra de desplazamiento (control de formulario) al lado de nuestro gráfico... incorporándole las siguientes propiedades:
Valor mínimo: 3
Valor máximo: 20
Vincular con Celda: $O$1
En la celda $O$2 añadimos la fórmula siguiente:
=INDICE(Radial!$Q$3:$Q$20;COINCIDIR(Radial!$O$1;Radial!$R$3:$R$20;0))
que nos permite recuperar el nombre del polígono...
De manera opcional podemos incorporarlo a nuestro Título del gráfico; para lo cual basta seleccionar el título y escribir en la barra de fórmulas la referencia:
=Radial!$O$2
Listo, ya solo tenemos que jugar con nuestra barra de desplazamiento para ver cómo toman cuerpo nuestros polígonos...
En primer lugar, a modo didáctico, recordaremos los nombres de los diferentes polígonos... (leer algo más en wikipedia):
| Clasificación de polígonos | |
|---|---|
| Nombre | n.º lados |
| trígono o triángulo | 3 |
| tetrágono, cuadrángulo o cuadrilátero | 4 |
| pentágono | 5 |
| hexágono | 6 |
| heptágono | 7 |
| octógono u octágono | 8 |
| eneágono o nonágono | 9 |
| decágono | 10 |
| endecágono o undecágono | 11 |
| dodecágono | 12 |
| tridecágono | 13 |
| tetradecágono | 14 |
| pentadecágono o pentedecágono | 15 |
| hexadecágono | 16 |
| heptadecágono | 17 |
| octodecágono u octadecágono | 18 |
| eneadecágono o nonadecágono | 19 |
| isodecágono o icoságono | 20 |
El objetivo es lograr lo siguiente:
Para la construcción en primer lugar dispondremos en un rango de una fila un mismo valor repetido, en mi caso en el rango T1:AM1 dispuse el valor 2 repetido veinte veces....
En segundo lugar seleccionando ese rango insertamos un gráfico tipo Radial.
A continuación eliminamos la etiqueta del eje radial y las líneas de división principal.
Un paso después crearemos el siguiente Nombre Definido:
lados =DESREF(Radial!$T$1;;;1;Radial!$O$1)
que tomará un número determinado de valores según se indique en la celda O1 (que más adelante indentificaremos).
En un paso posterior seleccionamos accedemos a la opción Selección de datos, y Editamos la Serie representada.
Incluimos en esta serie el Nombre definido anterior:
Añadimos ahora una Barra de desplazamiento (control de formulario) al lado de nuestro gráfico... incorporándole las siguientes propiedades:
Valor mínimo: 3
Valor máximo: 20
Vincular con Celda: $O$1
En la celda $O$2 añadimos la fórmula siguiente:
=INDICE(Radial!$Q$3:$Q$20;COINCIDIR(Radial!$O$1;Radial!$R$3:$R$20;0))
que nos permite recuperar el nombre del polígono...
De manera opcional podemos incorporarlo a nuestro Título del gráfico; para lo cual basta seleccionar el título y escribir en la barra de fórmulas la referencia:
=Radial!$O$2
Listo, ya solo tenemos que jugar con nuestra barra de desplazamiento para ver cómo toman cuerpo nuestros polígonos...





Excelente solucion. Gracias
ResponderEliminar