Ayer día 20 de diciembre de 2015 se celebraron Elecciones a Cortes Generales y como siempre escuchamos el nombre de un tal 'Victor d'Hondt' para explicar la atribución o reparto de escaños en el parlamento.
Trataré de exponer aquí cuál es el modelo de reparto de acuerdo a la Ley electoral española (basada en el sistema d'Hondt).
Lo importante, al respecto, es el artículo 163 de la Ley Orgánica 5/1985, de 19 de junio, que dice:
La verdad es que el sistema está muy claramente explicado en el artículo anterior, y sin entrar en justicias-injusticias o distorsiones de éste, veremos cómo nos puede ayudar Excel a obtener el dato buscado: Reparto del número de escaños de una circunscripción.
Si te interesa puedes leer algo más del sistema d'Hondt aquí
Veamos un caso real según los datos de mi circunscripción electoral: Madrid.
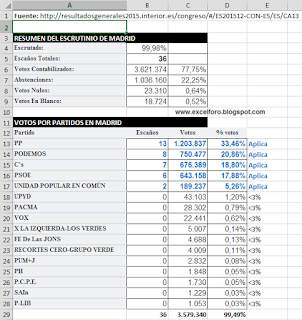
Los datos de votos han sido (Fuente: Ministerio del Interior)
Como vemos el número de escaños a repartir es de 36. Por otro lado el número de partidos que verifican el artículo 163.1.a de la ley electoral (Ley Orgánica 5/1985, de 19 de junio) y superan el 3% de los votos se reduce a 5 partidos.
Por tanto, según la norma de reparto, siguiendo el modelo descrito en ese mismo artículo, montaremos una Tabla de referencia cruzada, tal como vemos en la imagen siguiente:
la fórmula de reparto en cada columna, para cada partido, consiste en dividir el número de votos obtenido entre el número de escaño que aparece en la columna E (en la imagen).
Como primera forma de ver el reparto podemos aplicar un Formato condicional sobre el rango de cálculos F3:J38, aplicando la regla condicional de los 36 valores superiores:
Observamos cómo quedan remarcados en 'verde' el número de escaños conseguido pro cada partido.
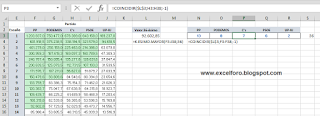
Otra forma de llegar al número de escaños consistiría en emplear las funciones K.ESIMO.MAYOR y COINCIDIR.
Calculamos y obtenemos en la celda L3 el valor que ocupa, dentro del rango de valores de nuestra matriz, la posición 36:
=K.ESIMO.MAYOR(F3:J38;36)
este será nuestro punto de referencia, ya que los cocientes obtenidos por encima de este valor serán los que nos interesen para descubrir el número de escaños de cada partido.
En las celdas N3:R3 aplicamos la función COINCIDIR, pero utilizando el tercer argumento 'Mayor que (-1)' sobre cada uno de los rangos de cada partido:
=COINCIDIR($L$3;F3:F38;-1)
con este argumento forzamos a COINCIDIR a encontrar el menor valor que es mayor o igual que el valor_buscado.
OJO, ya que los valores del argumento matriz_buscada deben estar en orden descendente... como en nuestro caso.
Con esta fórmula obtenemos la posición del valor/cociente buscado, y por ende, del número de escaños correspondiente.
Trataré de exponer aquí cuál es el modelo de reparto de acuerdo a la Ley electoral española (basada en el sistema d'Hondt).
Lo importante, al respecto, es el artículo 163 de la Ley Orgánica 5/1985, de 19 de junio, que dice:
| 1. La atribución de los escaños en función de los resultados del escrutinio se realiza conforme a las siguientes reglas: a) No se tienen en cuenta aquellas candidaturas que no hubieran obtenido, al menos, el 3 por 100 de los votos válidos emitidos en la circunscripción. b) Se ordenan de mayor a menor, en una columna, las cifras de votos obtenidos por las restantes candidaturas. c) Se divide el número de votos obtenidos por cada candidatura por 1, 2, 3, etc., hasta un número igual al de escaños correspondientes a la circunscripción, formándose un cuadro similar al que aparece en el ejemplo práctico. Los escaños se atribuyen a las candidaturas que obtengan los cocientes mayores en el cuadro, atendiendo a un orden decreciente. Ejemplo práctico: 480.000 votos válidos emitidos en una circunscripción que elija ocho Diputados. Votación repartida entre seis candidaturas: A(168.000 votos) B(104.000) C(72.000) D(64.000) E(40.000) F(32.000) División 1 2 3 4 5 6 7 8 A 168.000 84.000 56.000 42.000 33.600 28.000 24.000 21.000 B 104.000 52.000 34.666 26.000 20.800 17.333 14.857 13.000 C 72.000 36.000 24.000 18.000 14.400 12.000 10.285 9.000 D 64.000 32.000 21.333 16.000 12.800 10.666 9.142 8.000 E 40.000 20.000 13.333 10.000 8.000 6.666 5.714 5.000 F 32.000 16.000 10.666 8.000 6.400 5.333 4.571 4.000 Por consiguiente: la candidatura A obtiene cuatro escaños. La candidatura B dos escaños y las candidaturas C y D un escaño cada una. d) Cuando en la relación de cocientes coincidan dos correspondientes a distintas candidaturas, el escaño se atribuirá a la que mayor número total de votos hubiese obtenido. Si hubiera dos candidaturas con igual número total de votos, el primer empate se resolverá por sorteo y los sucesivos de forma alternativa. e) Los escaños correspondientes a cada candidatura se adjudican a los candidatos incluidos en ella, por el orden de colocación en que aparezcan. |
La verdad es que el sistema está muy claramente explicado en el artículo anterior, y sin entrar en justicias-injusticias o distorsiones de éste, veremos cómo nos puede ayudar Excel a obtener el dato buscado: Reparto del número de escaños de una circunscripción.
Si te interesa puedes leer algo más del sistema d'Hondt aquí
Veamos un caso real según los datos de mi circunscripción electoral: Madrid.
Los datos de votos han sido (Fuente: Ministerio del Interior)
Como vemos el número de escaños a repartir es de 36. Por otro lado el número de partidos que verifican el artículo 163.1.a de la ley electoral (Ley Orgánica 5/1985, de 19 de junio) y superan el 3% de los votos se reduce a 5 partidos.
Por tanto, según la norma de reparto, siguiendo el modelo descrito en ese mismo artículo, montaremos una Tabla de referencia cruzada, tal como vemos en la imagen siguiente:
la fórmula de reparto en cada columna, para cada partido, consiste en dividir el número de votos obtenido entre el número de escaño que aparece en la columna E (en la imagen).
Como primera forma de ver el reparto podemos aplicar un Formato condicional sobre el rango de cálculos F3:J38, aplicando la regla condicional de los 36 valores superiores:
Observamos cómo quedan remarcados en 'verde' el número de escaños conseguido pro cada partido.
Otra forma de llegar al número de escaños consistiría en emplear las funciones K.ESIMO.MAYOR y COINCIDIR.
Calculamos y obtenemos en la celda L3 el valor que ocupa, dentro del rango de valores de nuestra matriz, la posición 36:
=K.ESIMO.MAYOR(F3:J38;36)
este será nuestro punto de referencia, ya que los cocientes obtenidos por encima de este valor serán los que nos interesen para descubrir el número de escaños de cada partido.
En las celdas N3:R3 aplicamos la función COINCIDIR, pero utilizando el tercer argumento 'Mayor que (-1)' sobre cada uno de los rangos de cada partido:
=COINCIDIR($L$3;F3:F38;-1)
con este argumento forzamos a COINCIDIR a encontrar el menor valor que es mayor o igual que el valor_buscado.
OJO, ya que los valores del argumento matriz_buscada deben estar en orden descendente... como en nuestro caso.
Con esta fórmula obtenemos la posición del valor/cociente buscado, y por ende, del número de escaños correspondiente.




No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.