Tiempo atrás vimos cómo construir un vistoso reloj 'literal' (ver).
En el día de hoy aprenderemos a construir un reloj analógico en Excel, lo que conseguiremos con un gráfico tipo dispersión, al que posteriormente agregaremos un procedimiento Sub (una macro) para que nuestras manecillas se mueven de acuerdo al paso del tiempo...
Lo primero será insertar un Gráfico de dispersión con líneas rectas y marcadores (o sólo con líneas rectas.. según el gusto). Lo haremos sin marcar ningún rango!!.
A este gráfico le cambiaremos el nombre y llamaremos 'GraficoAnalogico':
Recordemos que este tipo de gráfico de dispersión nos pide un valor para el eje X y otro para el eje Y, con el que construimos el par ordenado que representa un punto en nuestro plano...
En el siguiente paso agregaremos tres series de datos desde Seleccionar Datos, a las que llamaremos: 'Secundero', 'Minutero' y 'Horas', sin incorporar ningún valor X o Y en ellos:
Repetimos la misma acción para las otras dos series... con lo que tendremos:
Repito, todas ellas con los valores por defecto (vacío para X y {1} para Y)...
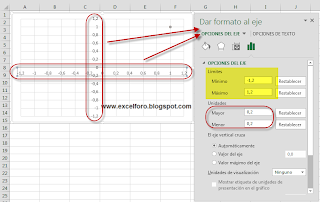
En la siguiente etapa configuramos las etiquetas de ambos ejes, para conseguir que el punto (0,0) quede en el centro del gráfico... para ello desde Dar formato al eje modificamos las Opciones del eje en cuanto a sus límites, dejándolo en el intervalo -1,2 a 1,2 .. para el eje horizontal y eje vertical:
Cuadramos visualmente nuestro gráfico.. por ejemplo, con una dimensión:
alto:=12,7 cm
ancho:=14,8 cm
por supuesto, al gusto del usuario...
Siguiente etapa... agregamos etiquetas de datos a nuestras tres series.. pero sólo al punto exterior, NO al punto (0,0)... podemos Agregarlo y luego borrarlo.
Incorporamos en un módulo de nuestro proyecto VBA los siguientes procedimientos:
Añadimos un par de botones de fórmulario para controlar el Comienzo y Parada de nuestro Reloj, a los que le asignamos las macros 'InicioReloj' y 'ParadaReloj':
Listos!!. Presionamos 'Inicio Reloj' y magia 'Excel':
Por supuesto a partir de aquí podemos 'maquetearlo' como mejor nos convenga.. con formas, colores, etc...
Pero sin duda, la clave para obtener nuestro reloj analógico es la forma en que hemos construido los pares de puntos (las manecillas), en las que hemos utilizado las funciones trigonométricas SIN (seno) y COS (coseno) para conseguir el efecto de movimiento a lo largo de una circunferencia. Por ejemplo, para el secundero nuestros cálculos han sido:
x(0) = 0
x(1) = 0.99 * Sin(Second(Time) * (2 * PI / 60))
y(0) = 0
y(1) = 0.99 * Cos(Second(Time) * (2 * PI / 60))
con el que convertíamos el segundo del momento Time, tratándolo por el resultado de 2*PI/60, esto es 2*Pi dividido por el número de segundos (60 s) en una circunferencia completa.
El 0,99 sólo nos aporta el largo final del vector conseguido...
De manera similar para la menecilla de las horas:
x(0) = 0
x(1) = 0.4 * Sin((Hour(Time) + (Minute(Time) / 60)) * (2 * PI / 12))
y(0) = 0
y(1) = 0.4 * Cos((Hour(Time) + (Minute(Time) / 60)) * (2 * PI / 12))
donde con la hora y 'pico' (horas + minutos transcurridos), la tratabamos por el resultado de 2*PI/12, i.e., 2*Pi dividido por el número de horas (12 horas) en una circunferencia completa.
En definitiva convertimos la linealidad en curva...
En el día de hoy aprenderemos a construir un reloj analógico en Excel, lo que conseguiremos con un gráfico tipo dispersión, al que posteriormente agregaremos un procedimiento Sub (una macro) para que nuestras manecillas se mueven de acuerdo al paso del tiempo...
Lo primero será insertar un Gráfico de dispersión con líneas rectas y marcadores (o sólo con líneas rectas.. según el gusto). Lo haremos sin marcar ningún rango!!.
A este gráfico le cambiaremos el nombre y llamaremos 'GraficoAnalogico':
Recordemos que este tipo de gráfico de dispersión nos pide un valor para el eje X y otro para el eje Y, con el que construimos el par ordenado que representa un punto en nuestro plano...
En el siguiente paso agregaremos tres series de datos desde Seleccionar Datos, a las que llamaremos: 'Secundero', 'Minutero' y 'Horas', sin incorporar ningún valor X o Y en ellos:
Repetimos la misma acción para las otras dos series... con lo que tendremos:
Repito, todas ellas con los valores por defecto (vacío para X y {1} para Y)...
En la siguiente etapa configuramos las etiquetas de ambos ejes, para conseguir que el punto (0,0) quede en el centro del gráfico... para ello desde Dar formato al eje modificamos las Opciones del eje en cuanto a sus límites, dejándolo en el intervalo -1,2 a 1,2 .. para el eje horizontal y eje vertical:
Cuadramos visualmente nuestro gráfico.. por ejemplo, con una dimensión:
alto:=12,7 cm
ancho:=14,8 cm
por supuesto, al gusto del usuario...
Siguiente etapa... agregamos etiquetas de datos a nuestras tres series.. pero sólo al punto exterior, NO al punto (0,0)... podemos Agregarlo y luego borrarlo.
Incorporamos en un módulo de nuestro proyecto VBA los siguientes procedimientos:
Dim Paso As Double
Sub InicioReloj()
ActualizaReloj
End Sub
Sub ParadaReloj()
'Cancela el eventoe OnTime y para nuestro Reloj analógico
On Error Resume Next
Application.OnTime Paso, "ActualizaReloj", , False
End Sub
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
Sub ActualizaReloj()
'Actualizamos nuestro reloj
Dim Reloj As Chart
Set Reloj = Sheets(1).ChartObjects("GraficoAnalogico").Chart
'PARÁMETROS RELOJ ANALÓGICO
Const PI As Double = 3.14159265358979
Dim SeriesGrafico As Series
Dim s As Series
'definimos dos matrices para construir los vectores
'que representarán las manecillas del reloj....
'Array x para los valores X de las series
Dim x(0 To 1) As Variant
'Array y para los valores Y de las series
Dim y(0 To 1) As Variant
'Secundero
Set SeriesGrafico = Reloj.FullSeriesCollection("Secundero")
'construimos el vector para los segundos
x(0) = 0
x(1) = 0.99 * Sin(Second(Time) * (2 * PI / 60))
y(0) = 0
y(1) = 0.99 * Cos(Second(Time) * (2 * PI / 60))
'asignamos un par a los valores de X de la Serie Secundero
SeriesGrafico.XValues = x
'asignamos un par a los valores de Y de la Serie Secundero
SeriesGrafico.Values = y
'completamos la etiqueta de datos con la lectura de los segundos....
SeriesGrafico.Points(2).DataLabel.Text = Second(Time) & " s"
'Minutero
Set SeriesGrafico = Reloj.FullSeriesCollection("Minutero")
'construimos el vector para los minutos
x(0) = 0
x(1) = 0.8 * Sin((Minute(Time) + (Second(Time) / 60)) * (2 * PI / 60))
y(0) = 0
y(1) = 0.8 * Cos((Minute(Time) + (Second(Time) / 60)) * (2 * PI / 60))
'asignamos un par a los valores de X de la Serie Minutero
SeriesGrafico.XValues = x
'asignamos un par a los valores de Y de la Serie Minutero
SeriesGrafico.Values = y
'completamos la etiqueta de datos con la lectura de los minutos....
SeriesGrafico.Points(2).DataLabel.Text = Minute(Time) & " m"
'Manecilla de las horas
Set SeriesGrafico = Reloj.FullSeriesCollection("Horas")
'construimos el vector para las horas
x(0) = 0
x(1) = 0.4 * Sin((Hour(Time) + (Minute(Time) / 60)) * (2 * PI / 12))
y(0) = 0
y(1) = 0.4 * Cos((Hour(Time) + (Minute(Time) / 60)) * (2 * PI / 12))
'asignamos un par a los valores de Y de la Serie Horas
SeriesGrafico.XValues = x
'asignamos un par a los valores de Y de la Serie Horas
SeriesGrafico.Values = y
'completamos la etiqueta de datos con la lectura de las horas....
SeriesGrafico.Points(2).DataLabel.Text = Hour(Time) & " hr"
'Configuramos cada nuevo paso del reloj cada segundo,
'lo que controlamos con TimeValue
Paso = Now + TimeValue("00:00:01")
Application.OnTime Paso, "ActualizaReloj"
End SubAñadimos un par de botones de fórmulario para controlar el Comienzo y Parada de nuestro Reloj, a los que le asignamos las macros 'InicioReloj' y 'ParadaReloj':
Listos!!. Presionamos 'Inicio Reloj' y magia 'Excel':

Por supuesto a partir de aquí podemos 'maquetearlo' como mejor nos convenga.. con formas, colores, etc...
Pero sin duda, la clave para obtener nuestro reloj analógico es la forma en que hemos construido los pares de puntos (las manecillas), en las que hemos utilizado las funciones trigonométricas SIN (seno) y COS (coseno) para conseguir el efecto de movimiento a lo largo de una circunferencia. Por ejemplo, para el secundero nuestros cálculos han sido:
x(0) = 0
x(1) = 0.99 * Sin(Second(Time) * (2 * PI / 60))
y(0) = 0
y(1) = 0.99 * Cos(Second(Time) * (2 * PI / 60))
con el que convertíamos el segundo del momento Time, tratándolo por el resultado de 2*PI/60, esto es 2*Pi dividido por el número de segundos (60 s) en una circunferencia completa.
El 0,99 sólo nos aporta el largo final del vector conseguido...
De manera similar para la menecilla de las horas:
x(0) = 0
x(1) = 0.4 * Sin((Hour(Time) + (Minute(Time) / 60)) * (2 * PI / 12))
y(0) = 0
y(1) = 0.4 * Cos((Hour(Time) + (Minute(Time) / 60)) * (2 * PI / 12))
donde con la hora y 'pico' (horas + minutos transcurridos), la tratabamos por el resultado de 2*PI/12, i.e., 2*Pi dividido por el número de horas (12 horas) en una circunferencia completa.
En definitiva convertimos la linealidad en curva...







No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.