En una entrada anterior vimos cómo conseguir un listado de las combinaciones de varios elementos, respondiendo a una estructura muy concreta...
En la entrada de hoy veremos, rindiendo homenaje a Myrna Larson, su magnífico código VBA que lista las combinaciones o permutaciones en nuestra hoja de Excel.
Es importante conocer las diferencias entre ambos conceptos, por lo que dejaré aquí un par de vínculos a Wikipedia:
Permutaciones (ver)
Combinaciones (ver)
Variaciones (ver)
A modo de resumen, una Permutación es la variación del orden o disposición de los elementos de un conjunto dado; mientras que una Combinación es la variación de número de formas en que se pueden extraer subconjuntos a partir de un conjunto dado, esto es, sin importar el orden o disposición.
Si el orden no importa, es una combinación.
Si el orden sí importa es una permutación.
Como siempre dejo explicaciones más concretas a los especialistas en el tema...
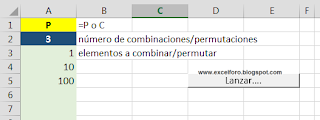
El código propuesto por Myrna (al que he modificado mínimamente para su correcto funcionamiento en Excel 2007 y +), funciona a partir de la indicación dispuesta en la celda A1 (P si deseamos ver las Permutaciones o C si Combinaciones). En A2 introduciremos el subconjunto de elementos que queremos ver (2 si queremos ver subconjuntos de dos elementos, 3 de tres, etc). Y a partir de A3 añadiremos los elementos a Permutar/Combinar.
Para ejecutar la macro de Myrna añadiremos un botón al que hemos asignado la macro llamada: 'ListPermutations'
Incorporaremos el código en un módulo de nuestro Proyecto de VB:
Si sobre el ejemplo de la imagen anterior Lanzamos la macro, obtendremos un listado como el siguiente:
1, 10, 100
1, 100, 10
10, 1, 100
10, 100, 1
100, 1, 10
100, 10, 1
Como vemos son las Permutaciones de los tres elementos dados {1, 10 , 100} tomados en subconjuntos de tres elementos.
Toca ahora cómo conseguir lo mismo, sin programación, pero con Access.
Abriremos una Base de datos y añadiremos/crearemos una Tabla con un campo:
A continuación crearemos una consulta con la siguiente estructura:
Importante observar que hemos incluido la misma Tabla2 tres veces y sin NINGUNA relación entre ellas. También es importante notar que los campos mostrados en la consulta corresponden uno a cada una de las tres tablas (repetidas)...NUNCA podrían provenir de una única Tabla!!.
Adicionalmente, al hablar de Permutaciones, añadimos un Campo Calculado, que he llamado 'Check', con la siguiente fórmula:
Check: SiInm([Tabla2].[Datos001]=[Tabla2_1].[Datos001] O [Tabla2].[Datos001]=[Tabla2_2].[Datos001] O [Tabla2_1].[Datos001]=[Tabla2_2].[Datos001];"repetido";"valido")
Campo sobre el que he aplicado un filtro para que muestre sólo los registros obtenidos que nos interesan...
Al ejecutar nuestra consulta obtendremos lo siguiente:
En definitiva, el mismo resultado que con el código de Permutaciones de Myrna Larson.
Dos maneras diferentes, con dos aplicaciones distintas de conseguir lo que pretendíamos.
En la entrada de hoy veremos, rindiendo homenaje a Myrna Larson, su magnífico código VBA que lista las combinaciones o permutaciones en nuestra hoja de Excel.
Es importante conocer las diferencias entre ambos conceptos, por lo que dejaré aquí un par de vínculos a Wikipedia:
Permutaciones (ver)
Combinaciones (ver)
Variaciones (ver)
A modo de resumen, una Permutación es la variación del orden o disposición de los elementos de un conjunto dado; mientras que una Combinación es la variación de número de formas en que se pueden extraer subconjuntos a partir de un conjunto dado, esto es, sin importar el orden o disposición.
Si el orden no importa, es una combinación.
Si el orden sí importa es una permutación.
Como siempre dejo explicaciones más concretas a los especialistas en el tema...
El código propuesto por Myrna (al que he modificado mínimamente para su correcto funcionamiento en Excel 2007 y +), funciona a partir de la indicación dispuesta en la celda A1 (P si deseamos ver las Permutaciones o C si Combinaciones). En A2 introduciremos el subconjunto de elementos que queremos ver (2 si queremos ver subconjuntos de dos elementos, 3 de tres, etc). Y a partir de A3 añadiremos los elementos a Permutar/Combinar.
Para ejecutar la macro de Myrna añadiremos un botón al que hemos asignado la macro llamada: 'ListPermutations'
Incorporaremos el código en un módulo de nuestro Proyecto de VB:
Dim vAllItems As Variant
Dim Buffer() As String
Dim BufferPtr As Long
Dim Results As Worksheet
'
' Posted by Myrna Larson
' July 25, 2000
' Microsoft.Public.Excel.Misc
' Subject: Combin
Sub ListPermutations()
Dim Rng As Range
Dim PopSize As Long 'Integer
Dim SetSize As Integer
Dim Which As String
Dim N As Double
Const BufferSize As Long = 4096
Set Rng = Selection.Columns(1).Cells
If Rng.Cells.Count = 1 Then
Set Rng = Range(Rng, Rng.End(xlDown))
End If
PopSize = Rng.Cells.CountLarge - 2
If PopSize < 2 Then GoTo DataError
SetSize = Rng.Cells(2).Value
If SetSize > PopSize Then GoTo DataError
Which = UCase$(Rng.Cells(1).Value)
Select Case Which
Case "C"
N = Application.WorksheetFunction.Combin(PopSize, SetSize)
Case "P"
N = Application.WorksheetFunction.Permut(PopSize, SetSize)
Case Else
GoTo DataError
End Select
If N > Cells.CountLarge Then GoTo DataError
Application.ScreenUpdating = False
Set Results = Worksheets.Add
vAllItems = Rng.Offset(2, 0).Resize(PopSize).Value
ReDim Buffer(1 To BufferSize) As String
BufferPtr = 0
If Which = "C" Then
AddCombination PopSize, SetSize
Else
AddPermutation PopSize, SetSize
End If
vAllItems = 0
Application.ScreenUpdating = True
Exit Sub
DataError:
If N = 0 Then
Which = "Enter your data in a vertical range of at least 4 cells. " _
& String$(2, 10) _
& "Top cell must contain the letter C or P, 2nd cell is the number " _
& "of items in a subset, the cells below are the values from which " _
& "the subset is to be chosen."
Else
Which = "This requires " & Format$(N, "#,##0") & _
" cells, more than are available on the worksheet!"
End If
MsgBox Which, vbOKOnly, "DATA ERROR"
Exit Sub
End Sub
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
'AddPermutation
Private Sub AddPermutation(Optional PopSize As Long = 0, _
Optional SetSize As Integer = 0, _
Optional NextMember As Integer = 0)
Static iPopSize As Integer
Static iSetSize As Integer
Static SetMembers() As Integer
Static Used() As Integer
Dim i As Integer
If PopSize <> 0 Then
iPopSize = PopSize
iSetSize = SetSize
ReDim SetMembers(1 To iSetSize) As Integer
ReDim Used(1 To iPopSize) As Integer
NextMember = 1
End If
For i = 1 To iPopSize
If Used(i) = 0 Then
SetMembers(NextMember) = i
If NextMember <> iSetSize Then
Used(i) = True
AddPermutation , , NextMember + 1
Used(i) = False
Else
SavePermutation SetMembers()
End If
End If
Next i
If NextMember = 1 Then
SavePermutation SetMembers(), True
Erase SetMembers
Erase Used
End If
End Sub
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
'AddCombination
Private Sub AddCombination(Optional PopSize As Long = 0, _
Optional SetSize As Integer = 0, _
Optional NextMember As Integer = 0, _
Optional NextItem As Integer = 0)
Static iPopSize As Integer
Static iSetSize As Integer
Static SetMembers() As Integer
Dim i As Integer
If PopSize <> 0 Then
iPopSize = PopSize
iSetSize = SetSize
ReDim SetMembers(1 To iSetSize) As Integer
NextMember = 1
NextItem = 1
End If
For i = NextItem To iPopSize
SetMembers(NextMember) = i
If NextMember <> iSetSize Then
AddCombination , , NextMember + 1, i + 1
Else
SavePermutation SetMembers()
End If
Next i
If NextMember = 1 Then
SavePermutation SetMembers(), True
Erase SetMembers
End If
End Sub
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
'SavePermutation
Private Sub SavePermutation(ItemsChosen() As Integer, _
Optional FlushBuffer As Boolean = False)
Dim i As Integer, sValue As String
Static RowNum As Long, ColNum As Long
If RowNum = 0 Then RowNum = 1
If ColNum = 0 Then ColNum = 1
If FlushBuffer = True Or BufferPtr = UBound(Buffer()) Then
If BufferPtr > 0 Then
If (RowNum + BufferPtr - 1) > Rows.Count Then
RowNum = 1
ColNum = ColNum + 1
If ColNum > 256 Then Exit Sub
End If
Results.Cells(RowNum, ColNum).Resize(BufferPtr, 1).Value _
= Application.WorksheetFunction.Transpose(Buffer())
RowNum = RowNum + BufferPtr
End If
BufferPtr = 0
If FlushBuffer = True Then
Erase Buffer
RowNum = 0
ColNum = 0
Exit Sub
Else
ReDim Buffer(1 To UBound(Buffer))
End If
End If
'construct the next set
For i = 1 To UBound(ItemsChosen)
sValue = sValue & ", " & vAllItems(ItemsChosen(i), 1)
Next i
'and save it in the buffer
BufferPtr = BufferPtr + 1
Buffer(BufferPtr) = Mid$(sValue, 3)
End SubSi sobre el ejemplo de la imagen anterior Lanzamos la macro, obtendremos un listado como el siguiente:
1, 10, 100
1, 100, 10
10, 1, 100
10, 100, 1
100, 1, 10
100, 10, 1
Como vemos son las Permutaciones de los tres elementos dados {1, 10 , 100} tomados en subconjuntos de tres elementos.
Toca ahora cómo conseguir lo mismo, sin programación, pero con Access.
Abriremos una Base de datos y añadiremos/crearemos una Tabla con un campo:
A continuación crearemos una consulta con la siguiente estructura:
Importante observar que hemos incluido la misma Tabla2 tres veces y sin NINGUNA relación entre ellas. También es importante notar que los campos mostrados en la consulta corresponden uno a cada una de las tres tablas (repetidas)...NUNCA podrían provenir de una única Tabla!!.
Adicionalmente, al hablar de Permutaciones, añadimos un Campo Calculado, que he llamado 'Check', con la siguiente fórmula:
Check: SiInm([Tabla2].[Datos001]=[Tabla2_1].[Datos001] O [Tabla2].[Datos001]=[Tabla2_2].[Datos001] O [Tabla2_1].[Datos001]=[Tabla2_2].[Datos001];"repetido";"valido")
Campo sobre el que he aplicado un filtro para que muestre sólo los registros obtenidos que nos interesan...
Al ejecutar nuestra consulta obtendremos lo siguiente:
En definitiva, el mismo resultado que con el código de Permutaciones de Myrna Larson.
Dos maneras diferentes, con dos aplicaciones distintas de conseguir lo que pretendíamos.





No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.