Hace ya bastante tiempo, al inicio de mi aventura como Blogger, expuse un sencillo ejemplo de la función ESTIMACION.LINEAL (ver), y cómo construir una línea de regresión. Hoy avanzaremos sobre este tema y veremos cómo conseguir, apoyándonos en constantes matriciales, una ecuación polinómica de regresión de diferente orden o grado.
En este ejemplo hay varias fórmulas que complementan nuestro objetivo, pero iremos por partes, centrándonos en la manera de conseguir nuestro polinomio.
Empecemos por los datos a partir de los cuales obtendremos nuestra ecuación. Los datos de la variable independiente 'datos_x' están en el rango C3:C13; mientras que los de la variable Y dependiente 'datos_y' los hallamos en el rango de celdas B3:B13.
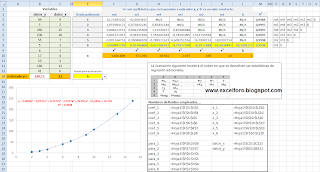
El objetivo es, según nuestra elección en la celda E14, conseguir el polinomio que represente la línea de tendencia, de grado 1 a 6, junto a su coeficiente de determinación R2, y a partir de la ecuación el valor estimado de y. Lo que se muestra en la imagen en las celdas F3:M8.
Importante también el uso de los nombres definidos, que serán los siguientes.
Para los datos del origen:
datos_x =Hoja1!$C$3:$C$13
datos_y =Hoja1!$B$3:$B$13
Para los coeficientes de las futuras ecuaciones:
coef_1 =Hoja1!$F$3:$G$3
coef_2 =Hoja1!$F$4:$H$4
coef_3 =Hoja1!$F$5:$I$5
coef_4 =Hoja1!$F$6:$J$6
coef_5 =Hoja1!$F$7:$K$7
coef_6 =Hoja1!$F$8:$L$8
Para los valores de las potencias del valor x a estimar:
x_1 =Hoja1!$K$10:$L$10
x_2 =Hoja1!$J$10:$L$10
x_3 =Hoja1!$I$10:$L$10
x_4 =Hoja1!$H$10:$L$10
x_5 =Hoja1!$G$10:$L$10
x_6 =Hoja1!$F$10:$L$10
Para ajustar el texto del encabezado en F2:L2:
para_1 =Hoja1!$P$8:$V$8
para_2 =Hoja1!$P$7:$V$7
para_3 =Hoja1!$P$6:$V$6
para_4 =Hoja1!$P$5:$V$5
para_5 =Hoja1!$P$4:$V$4
para_6 =Hoja1!$P$3:$V$3
Lógicamente no es el mismo número de parámetros de una ecuación de grado 1 que de grado 6, siendo sus formas:
Grado 1: y=mx + b (linea recta)
Grado 2: y=m2x2 + m1x + b (parábola)
Grado 3: y=m3x3 + m2x2 + m1x + b
etc...
Así, para la ecuación de la línea recta (grado1), seleccionaremos el rango F3:L3 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;datos_x)
Para la ecuación de grado 2 seleccionaremos el rango F4:L4 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2}))
Para la ecuación de grado 3 seleccionaremos el rango F5:L5 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3}))
Para la ecuación de grado 4 seleccionaremos el rango F6:L6 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3\4}))
Para la ecuación de grado 5 seleccionaremos el rango F7:L7 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3\4\5}))
Para la ecuación de grado 6 seleccionaremos el rango F8:L8 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3\4\5\6}))
Como vemos la estructura es similar para las diferentes ecuaciones, basta adaptar la constante matricial al grado del polinomio.
Para los valores potenciados de x dado para estimar y en el rango de celdas F10:L10 introducimos y ejecutamos matricialmente:
=POTENCIA($C$14;{6\5\4\3\2\1\0})
Para el cálculo del R2 para cada polinómio aplicamos la función INDICE a la función ESTIMACION.LINEAL, detallando qué 'estadístico' (qué situación) es el que nos interesa (fila 3 columna 1 de la matriz de estadísticos).
Por tanto para la ecuación de grado 1 tendríamos en la celda M3:
=INDICE(ESTIMACION.LINEAL(datos_y;datos_x;;1);3)
para la de grado 2 en M4:
=INDICE(ESTIMACION.LINEAL(datos_y;datos_x^{1\2};;1);3)
para la de grado 3 en M5:
=INDICE(ESTIMACION.LINEAL(datos_y;datos_x^{1\2\3};;1);3)
y sucesivamente hasta M8.
Con lo que tendríamos lo que buscamos, el valor y estimado para un x dado, según el grado del polinomio que nos interese seleccionándolo en la celda validada E14:
Vemos como del gráfico resultante (ajustado con macros) obtenemos la misma ecuación y el mismo coeficiente de determinación R2.
Finalmente en la celda B14 es donde hemos conseguido el valor de y estimado aplicando la función SUMAPRODUCTO, ajustándola al grado del polinomio seleccionado:
=SUMAPRODUCTO(INDIRECTO("coef_"&$E$14);INDIRECTO("x_"&$E$14))
donde vemos que realizamos el producto elemento a elemento y luego la suma de la matriz de coeficientes con los de los valores de x potenciados... es decir, donde conseguimos el producto y la suma posterior resultante de la ecuación del tipo:
y=m6x6 + ... +m3x3 + m2x2 + m1x + b
Otra forma de conseguirlo, sería empleando columnas auxiliares que representaran las potencias del valor x, como se ve en el ejemplo de la siguiente imagen para conseguir los coeficientes de la ecuación, al que hemos anexado el cálculo =B3^2 en el rango C3:C13:
En F3:J3 he añadido:
=ESTIMACION.LINEAL(A3:A13;B3:C13)
Vemos que con una función 'sencilla' ESTIMACION.LINEAL tomando como valores de x todas las columnas de x (x, x2) conseguimos los mismos datos que los calculados anteriormente...
Para ecuaciones de mayor grado bastaría agregar nuevas columnas auxiliares con la operación de potencia correspondiente x3, x4, etc... para luego incluirlas en la función ESTIMACION.LINEAL como parte del argumento 'datos de x'
En este ejemplo hay varias fórmulas que complementan nuestro objetivo, pero iremos por partes, centrándonos en la manera de conseguir nuestro polinomio.
Empecemos por los datos a partir de los cuales obtendremos nuestra ecuación. Los datos de la variable independiente 'datos_x' están en el rango C3:C13; mientras que los de la variable Y dependiente 'datos_y' los hallamos en el rango de celdas B3:B13.
El objetivo es, según nuestra elección en la celda E14, conseguir el polinomio que represente la línea de tendencia, de grado 1 a 6, junto a su coeficiente de determinación R2, y a partir de la ecuación el valor estimado de y. Lo que se muestra en la imagen en las celdas F3:M8.
Importante también el uso de los nombres definidos, que serán los siguientes.
Para los datos del origen:
datos_x =Hoja1!$C$3:$C$13
datos_y =Hoja1!$B$3:$B$13
Para los coeficientes de las futuras ecuaciones:
coef_1 =Hoja1!$F$3:$G$3
coef_2 =Hoja1!$F$4:$H$4
coef_3 =Hoja1!$F$5:$I$5
coef_4 =Hoja1!$F$6:$J$6
coef_5 =Hoja1!$F$7:$K$7
coef_6 =Hoja1!$F$8:$L$8
Para los valores de las potencias del valor x a estimar:
x_1 =Hoja1!$K$10:$L$10
x_2 =Hoja1!$J$10:$L$10
x_3 =Hoja1!$I$10:$L$10
x_4 =Hoja1!$H$10:$L$10
x_5 =Hoja1!$G$10:$L$10
x_6 =Hoja1!$F$10:$L$10
Para ajustar el texto del encabezado en F2:L2:
para_1 =Hoja1!$P$8:$V$8
para_2 =Hoja1!$P$7:$V$7
para_3 =Hoja1!$P$6:$V$6
para_4 =Hoja1!$P$5:$V$5
para_5 =Hoja1!$P$4:$V$4
para_6 =Hoja1!$P$3:$V$3
Lógicamente no es el mismo número de parámetros de una ecuación de grado 1 que de grado 6, siendo sus formas:
Grado 1: y=mx + b (linea recta)
Grado 2: y=m2x2 + m1x + b (parábola)
Grado 3: y=m3x3 + m2x2 + m1x + b
etc...
Así, para la ecuación de la línea recta (grado1), seleccionaremos el rango F3:L3 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;datos_x)
Para la ecuación de grado 2 seleccionaremos el rango F4:L4 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2}))
Para la ecuación de grado 3 seleccionaremos el rango F5:L5 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3}))
Para la ecuación de grado 4 seleccionaremos el rango F6:L6 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3\4}))
Para la ecuación de grado 5 seleccionaremos el rango F7:L7 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3\4\5}))
Para la ecuación de grado 6 seleccionaremos el rango F8:L8 e introduciremos y ejecutaremos matricialmente:
=ESTIMACION.LINEAL(datos_y;POTENCIA(datos_x;{1\2\3\4\5\6}))
Como vemos la estructura es similar para las diferentes ecuaciones, basta adaptar la constante matricial al grado del polinomio.
Para los valores potenciados de x dado para estimar y en el rango de celdas F10:L10 introducimos y ejecutamos matricialmente:
=POTENCIA($C$14;{6\5\4\3\2\1\0})
Para el cálculo del R2 para cada polinómio aplicamos la función INDICE a la función ESTIMACION.LINEAL, detallando qué 'estadístico' (qué situación) es el que nos interesa (fila 3 columna 1 de la matriz de estadísticos).
Por tanto para la ecuación de grado 1 tendríamos en la celda M3:
=INDICE(ESTIMACION.LINEAL(datos_y;datos_x;;1);3)
para la de grado 2 en M4:
=INDICE(ESTIMACION.LINEAL(datos_y;datos_x^{1\2};;1);3)
para la de grado 3 en M5:
=INDICE(ESTIMACION.LINEAL(datos_y;datos_x^{1\2\3};;1);3)
y sucesivamente hasta M8.
Con lo que tendríamos lo que buscamos, el valor y estimado para un x dado, según el grado del polinomio que nos interese seleccionándolo en la celda validada E14:

Vemos como del gráfico resultante (ajustado con macros) obtenemos la misma ecuación y el mismo coeficiente de determinación R2.
Finalmente en la celda B14 es donde hemos conseguido el valor de y estimado aplicando la función SUMAPRODUCTO, ajustándola al grado del polinomio seleccionado:
=SUMAPRODUCTO(INDIRECTO("coef_"&$E$14);INDIRECTO("x_"&$E$14))
donde vemos que realizamos el producto elemento a elemento y luego la suma de la matriz de coeficientes con los de los valores de x potenciados... es decir, donde conseguimos el producto y la suma posterior resultante de la ecuación del tipo:
y=m6x6 + ... +m3x3 + m2x2 + m1x + b
Otra forma de conseguirlo, sería empleando columnas auxiliares que representaran las potencias del valor x, como se ve en el ejemplo de la siguiente imagen para conseguir los coeficientes de la ecuación, al que hemos anexado el cálculo =B3^2 en el rango C3:C13:
En F3:J3 he añadido:
=ESTIMACION.LINEAL(A3:A13;B3:C13)
Vemos que con una función 'sencilla' ESTIMACION.LINEAL tomando como valores de x todas las columnas de x (x, x2) conseguimos los mismos datos que los calculados anteriormente...
Para ecuaciones de mayor grado bastaría agregar nuevas columnas auxiliares con la operación de potencia correspondiente x3, x4, etc... para luego incluirlas en la función ESTIMACION.LINEAL como parte del argumento 'datos de x'



Hola excelforo,
ResponderEliminarUna consulta quisiera saber que fórmula tiene la celda C14 y que me explique un poco de como haz realizado la gráfica que es dinámica con la validación de datos osea la celda E14, me gustaría saber que pasos has realizado.
de antemano gracias
atentamente
Ana
Saludos
Hola Ana,
Eliminaren C14 no hay ninguna fórmula es la variable independiente a partir de donde se calcula B14 (variable dependiente).
Respecto a la gráfica 'dinámica' lleva asociada programación, en concreto un evento Change, que se ejecuta al variar la celda E14.
En particular el código es:
Private Sub Worksheet_Change(ByVal Target As Range)
If Not Intersect(Target, Range("E14")) Is Nothing Then
If Range("E14").Value > 1 Then
ActiveSheet.ChartObjects("Gráfico 2").Activate
With ActiveChart.SeriesCollection(1).Trendlines(1)
.Type = xlPolynomial
.Order = Range("E14").Value
End With
Else
ActiveSheet.ChartObjects("Gráfico 2").Activate
With ActiveChart.SeriesCollection(1).Trendlines(1)
.Type = xlLinear
End With
End If
Range("E14").Select
End If
End Sub
Saludos
EN LA POTENCIA {1\2\3\4}, SON VALORES BALIDOS? POR QUE VALORES LOS SUSTITUYO?
EliminarHola Gusvo,
Eliminarque tal estás?.. un placer saludarte igualmente.
la matriz {1\2\3\4} representa los exponentes de los parámetros de una ecuación de cuarto grado... si requieres una línea polinómica de cuarto grado es lo que debes usar.
Un saludo y gracias por no escribir en mayúsculas.
Me parece que la otra opción es utilizar coma "," o, punto y coma ";". Yo intenté con "/" y con "\", pero no funcionó
EliminarHola Erick
Eliminarel poner coma, punto y como o las / o \ (dependiendo de las versiones) devuelve matrices en horizontal o vertical... lo que afecta al cálculo deseado
Saludos!
Gracias por la información, ¿podrías decirme qué signo afecta en qué dirección a la matriz, es decir, qué signo afecta o influye de forma horizontal y cuál en vertical?
EliminarHola
Eliminarorientación horizontal algo del tipo ={1;2;3;4}; o bien con una orientación vertical ={1\2\3\4}...
por supuesto, combinando ambos signos de puntuación, tendríamos una matriz de constantes bidimensional ={1;2;3\4;5;6}
slds
Wow, muchas gracias por la información Isma, será de mucha ayuda!
EliminarGracias!
EliminarHola Excelforo, muy buen aporte, me fue de gran utilidad seguir tus explicaciones. Pero tengo un problema, ya que quiero estimar un x de varias curvas para un valor y determinado y no se como hacerlo, con el comando objetivo no me sirve por tener diferentes curvas. Se puede solucionar de alguna manera??
ResponderEliminarHola Anselmo,
Eliminardiscúlpame pero no comprendo tu planteamiento...
a qué te refieres con el 'comando objetivo'???
Un saludo
Este comentario ha sido eliminado por el autor.
ResponderEliminarExcelente aporte, muchas gracias! ¿Cómo lograste el cambio automático en el encabezado?
ResponderEliminarGracias Jorge,
Eliminarel encabezado (celdas F2:L2) tienen una función matricial:
=SI(INDIRECTO("para_"&$E$14)=0;"";INDIRECTO("para_"&$E$14))
Un saludo
Nuevamente, muchas gracias, funciono perfecto! Aporte de mucha utilidad!
Eliminarestaria excelente tener el archivo de excel que elaboraste para solucionar todas las dudas y errores que me surgieron al realizarlo
ResponderEliminarHola Hector,
Eliminarcomo estás?, un placer saludarte igualmente...
Solo debes seguir los pasos descritos, si te surge alguna duda, por supuesto, puedes plantearla aquí.
Saludos
Este comentario ha sido eliminado por el autor.
ResponderEliminarque tal, ya he realizado el ejercicio, pero aun no me queda, tego duda en la celda C14 y de como hacer para que varien mis datos en los rangos de F:L de l renglon 3 al 8 ne funcion de la celda E14, me gustaria que vieras mi archivo, pero no se donde enviartelo
ResponderEliminartambién para el caso del rango F2:L2 no me hace el cambio, ya aplique la función matricial, pero me manda #Valor
ResponderEliminarHola Hector,
Eliminarpuedes enviarme el fichero a
excelforo@gmail.com
Saludos
gracias por ver mi fichero, lamentablemente te envíe mi primer versión, pero aun así con lo que me comentaste por correo logre recrear el ejemplo, gracias, igual ya comprendí que es el valor de C14, muy buen ejemplo, en mi caso, como reto, no tengo permitido usar código VBA para la gráfica, tienes alguna recomendación para hacer la sin el.
ResponderEliminar;-)
EliminarSin macros la actualización y cambio de tipo de línea se debería hacer manualmente
Saludos
Hola Ismael,
ResponderEliminarHe intentado seguir los pasos descritos, pero no consigo avanzar en el Excel, podrías enviarme el archivo?
Gracias de antemano
Hola Alejandro,
Eliminarlo siento, no guardo ficheros tan viejos
Intenta seguir los pasos, y comentas cualquier duda
Saludos
hola buenas tardes excelente tutotial, una consulta tendrias algun ejemplo tabla de excel para realizar el analisis de datos x & y para generar una funcion polinomica de 5 to grado?
ResponderEliminarHola Edgar,
Eliminaren este mismo post puedes ver cómo conseguir funciones polinómicas de hasta 6º grado... a partir de datos en x e y
¿Cúal es tu duda en concreto?
Slds
buenas noches, para preguntarte de donde sale el valor de c14. mil gracias
ResponderEliminarHola,
Eliminares cualquier dato introducido manualmente...
lo importante es B14 que responde al resultado de la fórmula descrita
Saludos
Hola Gustavo ingreando la expresión del grado 2 =ESTIMACION.LINEAL($B3:$B13,$C3:$C13,POTENCIA($C3:$C13,{1\2}))
ResponderEliminarme sale un error que no me reconoce {1\2}
tiene alguna cosa que cambie o me pueda ayudra a ejcutar
Hola,
EliminarNo se quién es ese 'Gustavo' a quien te diriges...
Pero me permito responderte yo, como creador del blog.
A veces, dependiendo de las versiones y configuración del Office cambia el separador de la \ por ; o incluso /
Saludos
A mi me ocurre el mismo caso me sale valor ya intente con \ y ; y nada que me sale no entiendo estoy con exel 2016
EliminarHola Jaime, qué tal estás?
Eliminarun placer saludarte igualmente
¿te has asegurado de ejecutarlo matricialmente?
Saludos
hola, este programa es modificable para funciones polinomicas de grado mayor a 6? imagino que si, pero no estoy segura, gracias
ResponderEliminarHola Macarena
Eliminarsí es posible... sol hay que trabajar los rangos y nombres definidos ajustándolos al nuevo 'grado' del polinómio
Slds
¡Hola Isma!
ResponderEliminarOye, seguí las instrucciones de tu blog y los números me quedaron iguales a los que muestras en las imágenes; sin embargo, cuando hice la gráfica dinámica, ésta me entrega una ecuación distinta cuando aplico la regresión polinomial de grado 6. Si no tienes inconveniente, ¿podría enviarte mi Excel para que me digas si hice algo mal, por favor?
Hola
Eliminarclaro, mi email:
excelforo@gmail.com
saludos
¡Muchas gracias por tu atención Ismael! Encontré la causa del error. Por lo que vi, la ecuación depende de si haces una gráfica dinámica o una gráfica normal. Al hacer la gráfica normal, la ecuación que te entrega es distinta.
EliminarGracias por tu tiempo para responder los mensajes.
;-)
Eliminaren realidad el gráfico es un gráfico normal de dispersión.. eso si es dinámico por que depende de datos variables en función de nuestra selección
Un saludo cordial!!
Me ayudó bastante tu información. ¡Gracias!
Eliminar;-)
Eliminarsaludos
Hola, Intenté calcular la formula de regresion polinominal (grado 6) que calcula el propio Excel para un gráfico con la formula estimacion.lineal pero no coincide. ¿Alguién sabe por qué? Debería dar la misma utilizando los mismos datos. ¿De donde puede venir la diferencia entre la calculada por mí mediante la formula estimacion.lineal y la calculada por el mismo MS Excel?
ResponderEliminarHola Carmelo
Eliminarla función ESTIMACION.LINEAL directamente solo te daría un grado seis si has añadido las seis columnas con el cálculo oportuno x^1, x^2, ..., x^6
Si has seguido los pasos, sí debería coincidir...
Alguna vez he hecho la prueba y si era correcto... sobre todo por que creo emplea el mismo algoritmo de cálculo.
Revisaría tu proceso de cálculo.
;-)
Saludos