Seguro que de niños alguna vez jugamos con un Espirógrafo (ver wikipedia). Ese juguete compuesto de varias reglas 'raras' que nos permitían realizar dibujos imposibles punteando con un lápiz.
Bien, pues aquellos dibujos, eran parte de complejas curvas matemáticas, con sus correspondientes fórmulas geométricas
En la entrada de hoy, a partir de una función geométrica, apoyada en diferentes parámetros, replicaremos el dibujo realizado por un Espirógrafo. Se hace necesario aplicar una macro que actualice los valores de nuestro dibujo, y simule nuestro lápiz sobre el papel y el extraño camino tomado...
Existen multitud de fórmulas geométricas, prácticamente todas basadas en cálculos con SEN y COSEN. Podemos ver algunas en nuestra amiga Wikipedia:
http://es.wikipedia.org/wiki/Epicicloide
http://es.wikipedia.org/wiki/Epitrocoide
En nuestro ejemplo emplearemos otra, que utiliza igualmente SEN y COSEN. ( la veremos más adelante).
La clave de todo nuestro ejemplo pasa por el empleo adecuado de Nombres definidos en su formato de fórmulas. Estas son todas las empleadas, prestando especial interés en las cuatro últimas:
p_1 =Espirografo!$B$11
p_2 =Espirografo!$B$12
p_3 =Espirografo!$B$13
r_1 =Espirografo!$B$3
r_2 =Espirografo!$B$4
r_3 =Espirografo!$B$5
s_1 =Espirografo!$B$7
s_2 =Espirografo!$B$8
s_3 =Espirografo!$B$9
t =(FILA(DESREF(Espirografo!$A$1;0;0;Espirografo!$B$1;1))- 1)*2*PI()/1000
tmax =MAX(t)
Xpoint =SI(Espirografo!$B$1>165;70;r_1*COS(2*PI()*s_1*tmax+p_1)+r_2*COS(2*PI()*s_2*tmax+p_2)+r_3*COS(2*PI()*s_3*tmax+p_3))
XSeries =r_1*COS(2*PI()*s_1*t+p_1)+r_2*COS(2*PI()*s_2*t+p_2)+r_3*COS(2*PI()*s_3*t+p_3)
Ypoint =r_1*SENO(2*PI()*s_1*tmax+p_1)+r_2*SENO(2*PI()*s_2*tmax+p_2)+r_3*SENO(2*PI()*s_3*tmax+p_3)
Yseries =r_1*SENO(2*PI()*s_1*t+p_1)+r_2*SENO(2*PI()*s_2*t+p_2)+r_3*SENO(2*PI()*s_3*t+p_3)
Veamos la disposición de los datos originales:
La macro, a insertar en un Módulo del Explorador de proyectos, dentro del Editor de VBA, sería:
Bien, pues aquellos dibujos, eran parte de complejas curvas matemáticas, con sus correspondientes fórmulas geométricas
En la entrada de hoy, a partir de una función geométrica, apoyada en diferentes parámetros, replicaremos el dibujo realizado por un Espirógrafo. Se hace necesario aplicar una macro que actualice los valores de nuestro dibujo, y simule nuestro lápiz sobre el papel y el extraño camino tomado...
Existen multitud de fórmulas geométricas, prácticamente todas basadas en cálculos con SEN y COSEN. Podemos ver algunas en nuestra amiga Wikipedia:
http://es.wikipedia.org/wiki/Epicicloide
http://es.wikipedia.org/wiki/Epitrocoide
En nuestro ejemplo emplearemos otra, que utiliza igualmente SEN y COSEN. ( la veremos más adelante).
La clave de todo nuestro ejemplo pasa por el empleo adecuado de Nombres definidos en su formato de fórmulas. Estas son todas las empleadas, prestando especial interés en las cuatro últimas:
p_1 =Espirografo!$B$11
p_2 =Espirografo!$B$12
p_3 =Espirografo!$B$13
r_1 =Espirografo!$B$3
r_2 =Espirografo!$B$4
r_3 =Espirografo!$B$5
s_1 =Espirografo!$B$7
s_2 =Espirografo!$B$8
s_3 =Espirografo!$B$9
t =(FILA(DESREF(Espirografo!$A$1;0;0;Espirografo!$B$1;1))- 1)*2*PI()/1000
tmax =MAX(t)
Xpoint =SI(Espirografo!$B$1>165;70;r_1*COS(2*PI()*s_1*tmax+p_1)+r_2*COS(2*PI()*s_2*tmax+p_2)+r_3*COS(2*PI()*s_3*tmax+p_3))
XSeries =r_1*COS(2*PI()*s_1*t+p_1)+r_2*COS(2*PI()*s_2*t+p_2)+r_3*COS(2*PI()*s_3*t+p_3)
Ypoint =r_1*SENO(2*PI()*s_1*tmax+p_1)+r_2*SENO(2*PI()*s_2*tmax+p_2)+r_3*SENO(2*PI()*s_3*tmax+p_3)
Yseries =r_1*SENO(2*PI()*s_1*t+p_1)+r_2*SENO(2*PI()*s_2*t+p_2)+r_3*SENO(2*PI()*s_3*t+p_3)
Veamos la disposición de los datos originales:
La macro, a insertar en un Módulo del Explorador de proyectos, dentro del Editor de VBA, sería:
Sub Dibujar()
'Iniciamos proceso con valores a cero
Range("B12").Value = 0
Range("B1").Value = 0
'Limitamos el contador en B1 hasta 150
While Range("B1").Value < 165
'Incrementamos el contador en B1 de uno en uno
Range("B1").Value = Range("B1").Value + 1
'añadiendo un retraso controlado con un FOR NEXT después de cada incremento en B1
For i = 1 To 150000
Next i
'Cede el control de la ejecución al sistema operativo,
'para que éste pueda procesar otros eventos.
'Permite la actualización del gráfico...
DoEvents
Wend
'Añadimos un extra en la animación
'Para ello incrementamos el contador en la variable B12
'Limitamos el contador en B4 hasta 10
While Range("B12").Value < 10
'Incrementamos el contador en B12 de 0.1 en 0.1
Range("B12").Value = Range("B12").Value + 0.1
'añadiendo un retraso controlado con un FOR NEXT después de cada incremento en B12
For i = 1 To 150000
Next i
'Cede el control de la ejecución al sistema operativo,
'para que éste pueda procesar otros eventos.
'Permite la actualización del gráfico...
DoEvents
Wend
End Sub
En este momento tenemos los datos, los cálculos realizados mediante las fórmulas en los Nombres definidos, y una macro que nos actualizará y simulará el movimiento, falta construir el Gráfico.
Lo primero que debemos saber es que nuestro gráfico debe ser de Tipo Dispersión con lineas suavizadas, es importante ya que necesitamos incluir dos variables, dos puntos (que hemos llamado XSeries e YSeries y también Xpoint e Ypoint).
Por pasos, desde el principio.
Desde la Ficha Insertar > grupo Gráficos > Dispersión > Dispersión con líneas suavizadas. Esto incluirá en blanco un objeto gráfico.
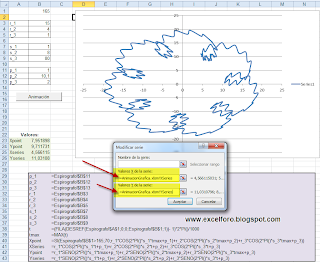
A continuación, desde la Barra de herramientas de gráficos > pestaña Diseño > grupo Datos > botón Seleccionar datos, y dentro de la venta diálogo, presionamos Agregar Serie. La completaremos con los valores siguientes:
para los Valores X de la serie: =AnimacionGrafica.xlsm!XSeries
para los Valores Y de la serie: =AnimacionGrafica.xlsm!YSeries
Ojo con esta forma de introducir Nombres definidos en un gráfico!!!.
Repetimos la operación para una segunda serie, pero ahora asignándole los valores:
para los Valores X de la serie: =AnimacionGrafica.xlsm!Xpoint
para los Valores Y de la serie: =AnimacionGrafica.xlsm!Ypoint
Siguiente paso a trabajar sobre el gráfico, fijamos las Escalas de los ejes (horizontal y vertical), bastará marcar a Fijo los valores dados:
Ya podemos seleccionar ambos ejes y suprimirlos, para que no se vean. Igualmente quitamos la Leyenda, damos formato de color al área del gráfico, color de las series, etc... hasta conseguir el aspecto que más nos guste. Y ya estamos en disposición de ejecutar nuestra macro llamada 'Dibujar' que hemos asignado a un botón. El efecto es el siguiente:

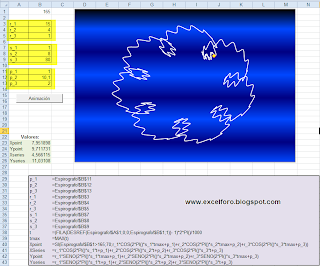




por que no dejas el archivo en .xls para bajar? seria mucho mas completo tu blog si así lo hicieras... saludos!!
ResponderEliminarHola, un placer saludarte igualmente.
EliminarPues es un problema de tiempo, de mantenimiento y en menor medida de dinero.
En todo caso, todos los ejemplos explicados puedes seguirlos perfectamente con las pautas especificadas.
Un saludo