Asignar un nombre a una fórmula en Excel.

Sí, has leído bien, no se trata de Asignar un nombre a un rango, si no de Asignar un nombre a una fórmula. La entrada de hoy explicará cuáles son las ventajas de dar nombres a nuestras fórmulas.
Como siempre, veámoslo con un ejemplo.
Tenemos una tabla de categorías con un valor correspondiente; y sobre estos valores tenemos un listado de 15 registros aleatorios:

Sobre este listado aleatorio encontraremos:

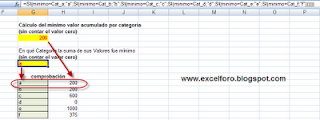
• Cálculo del minimo valor acumulado por categoría(sin contar el valor cero)


• En qué Categoría la suma de sus Valores fue mínimo(sin contar el valor cero)

Para responder ambas cuestiones, partiremos del mismo trabajo.
En primer lugar, por comodidad Asignaremos un nombre a los rangos del listado a evaluar:
Categoría =Hoja1!$D$3:$D$17
Valor =Hoja1!$E$3:$E$17

Ahora ya podemos construir una fórmula matricial a la que asignaremos un nombre.
Una para cada 'Categoría':
Cat_a =SUMA(SI(Categoría="a";Valor))
Cat_b =SUMA(SI(Categoría="b";Valor))
Cat_c =SUMA(SI(Categoría="c";Valor))
Cat_d =SUMA(SI(Categoría="d";Valor))
Cat_e =SUMA(SI(Categoría="e";Valor))
Cat_f =SUMA(SI(Categoría="f";Valor))

Es muy importante que nos fijemos en la estructura de fórmula matricial que hemos formado
=SUMA(SI(Categoría="a";Valor))
pero que está escrito normalmente; es decir, tenemos una matricial escrita como una función directa. Esta es una de las ventajas de trabajar Asignando nombres a fórmulas, si es menester. Ya tenemos el equivalente a seis funciones matriciales.
El siguiente paso, es atender las cuestiones planteadas.
La primera era: "Cálculo del minimo valor acumulado por categoría(sin contar el valor cero)", esto es, acumulando los valores para cada categoría, cuál es el menor importe, obviando el cero.
Nuestra fórmula será entonces:
=MIN(SI(Cat_a=0;5000;Cat_a);SI(Cat_b=0;5000;Cat_b);SI(Cat_c=0;5000;Cat_c);SI(Cat_d=0;5000;Cat_d);SI(Cat_e=0;5000;Cat_e);SI(Cat_f=0;5000;Cat_f))
¿Qué hemos calculado?. Para cada categoría hemos evaluado si su suma acumulada es cero, por que en ese caso, no la debemos contar en nuestro cálculo, es por eso que en caso de que sume cero, le damos un valor máximo de 5000.
Con la función MIN, obtenemos entonces el importe mínimo de las seis categorías.
Lo podemos comprobar en la imagen:

haz click en la imagen

Obtenido el primer valor, ahora buscaremos el segundo, es decir, a qué Categoría corresponde el valor acumulado mínimo.
Para ello, ya que disponemos del valor acumulado mínimo, aprovecharemos nuestro conocimiento, y Asignaremos nombre a nuestra fórmula anterior, le llamaremos 'minimo':
minimo =MIN(SI(Cat_a=0;5000;Cat_a);SI(Cat_b=0;5000;Cat_b);SI(Cat_c=0;5000;Cat_c);SI(Cat_d=0;5000;Cat_d);SI(Cat_e=0;5000;Cat_e);SI(Cat_f=0;5000;Cat_f))

Entonces, nuestra fórmula será en esta ocasión:
=SI(minimo=Cat_a;"a";SI(minimo=Cat_b;"b";SI(minimo=Cat_c;"c";SI(minimo=Cat_d;"d";SI(minimo=Cat_e;"e";SI(minimo=Cat_f;"f"))))))
Anidando diferentes SI condicionales, llegamos a la Categoría mínima.

Lo más importante es comprender, que esta forma de trabajar sólo nos aporta comodidad, que en este ejercicio, podríamos haber construido nuestras funciones escribiendo todas y cada una de las intrucciones, y ejecutándolas matricialmente hubiéramos llegado al mismo resultado.
Esta era la segunda gran ventaja, visualizamos mucho mejor las estructuras de nuestra fórmulas.